Your Graph coloring using backtracking example images are ready. Graph coloring using backtracking example are a topic that is being searched for and liked by netizens today. You can Download the Graph coloring using backtracking example files here. Download all free photos and vectors.
If you’re looking for graph coloring using backtracking example pictures information linked to the graph coloring using backtracking example interest, you have pay a visit to the ideal site. Our website always gives you suggestions for refferencing the highest quality video and picture content, please kindly surf and find more enlightening video articles and graphics that match your interests.
Graph Coloring Using Backtracking Example. Return false. Since each node can be coloured using any of the m available colours the total number of colour configurations possible are mV. Algorithm Algorithm solution for problem solved using BACKTRACKING are RECURSIVE The input to algorithm is vertex number present in the graph The algorithm generates the color number assigned to vertex and stores it an array. Print the solution printSolutioncolor.
Algorithm Unit 4 From slideshare.net
The colors are represented by the integers 1 2 m and the solutions are given by the n-tuple x1 x2 x3 xn where x1 is the color. This game is a variation of Graph coloring problem where every cell denotes a node or vertex and there exists an edge between two nodes if the nodes are in same row or same column or same block. So the order in which the vertices are picked is important. Proof by induction on the number of vertices. If N is a goal node return success 2. Since each node can be coloured using any of the m available colours the total number of colour configurations possible are mV.
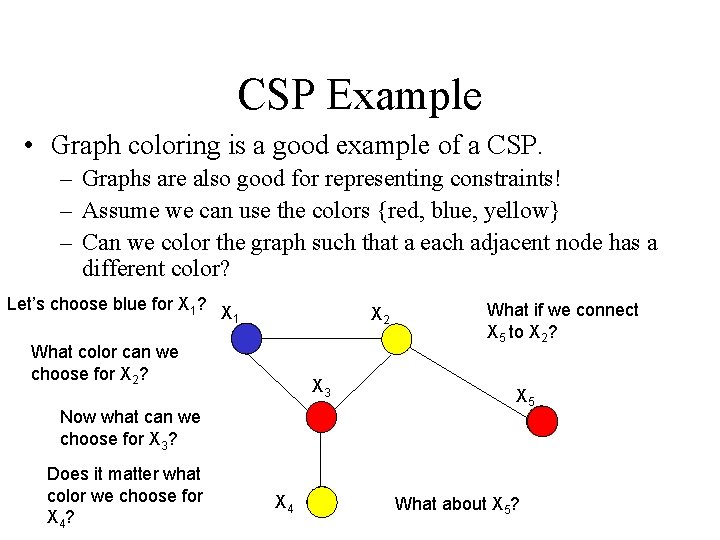
Graph coloring problem involves assigning colors to certain elements of a graph subject to certain restrictions and constraints.
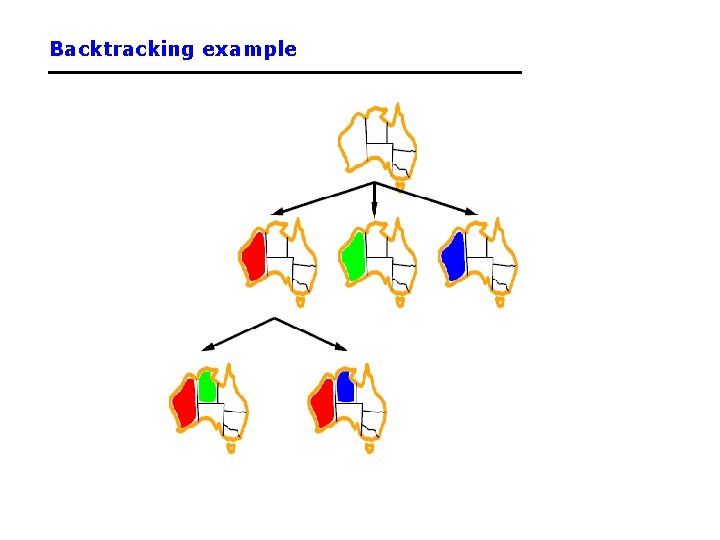
A The principal states and territories of Australia. At the end of this video in a MAP region 1 is also Adjacent to region 4 Graph coloring problem using BacktrackingPATREON. Backtracking Set 5 m Coloring Problem-Backtracking-Given an undirected graph and a number m determine if the graph can be colored with at most m colors. Note that in graph on right side vertices 3 and 4 are swapped. Graph Coloring Applications- Some important applications of graph coloring are as follows-Map Coloring. But if we consider the vertices 0 1 2 3 4 in right graph we need 4 colors.
Source: slideshare.net
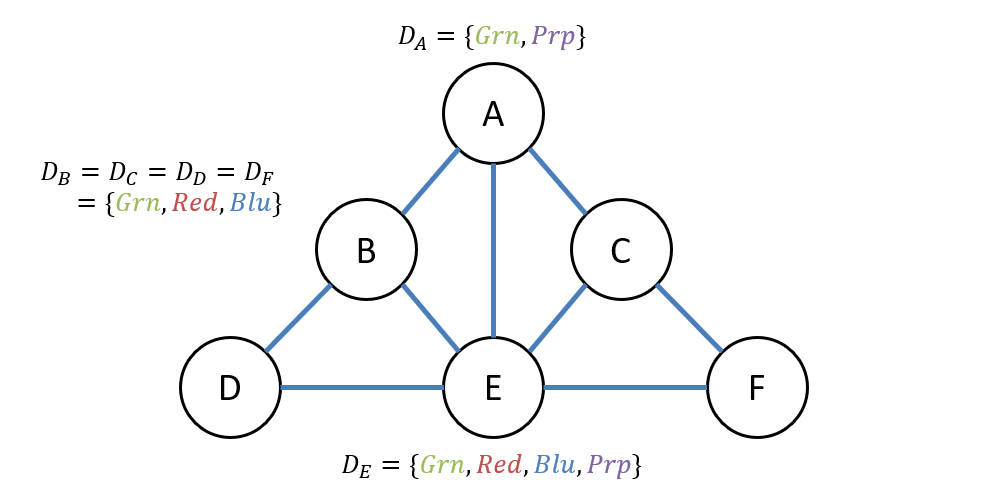
Graph Coloring Example- The following graph is an example of a properly colored graph- In this graph No two adjacent vertices are colored with the same color. If yes then color it and otherwise try a different color. I if graphvi. Since each node can be coloured using any of the m available colours the total number of colour configurations possible are mV. We strongly recommend that you click here and practice it before moving on to the solution.
Source: youtube.com
A utility function to print solution void printSolutionint color printfSolution Exists Following are the assigned colors. This game is a variation of the Graph coloring problem where every cell denotes a node or vertex and there exists an edge between two nodes if the nodes are in the same row or. Bool isSafe int v bool graphVV int color int c for int i 0. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Any connected simple planar graph with 5 or fewer vertices is 5colorable.
Source: tutorialspoint.dev
Algorithm Algorithm solution for problem solved using BACKTRACKING are RECURSIVE The input to algorithm is vertex number present in the graph The algorithm generates the color number assigned to vertex and stores it an array. For example consider the following two graphs. Method to Color a Graph. To explore node N. There will be Vm configurations of colors.
Source: slidetodoc.com
Graph Coloring Applications- Some important applications of graph coloring are as follows-Map Coloring. Four colors are chosen as - Red Green Blue and Yellow Now the map can be colored as shown here- 18. If graphColoringUtil graph m color v1 true return true. Bool graphColoringbool graphVV int m int color. The steps required to color a graph G with n number of vertices are as follows.
Source: slidetodoc.com
Proof by induction on the number of vertices. Call graphColoringUtil for vertex 0 if graphColoringUtilgraph m color 0 false printfSolution does not exist. To explore node N. For int i 0. Return false.
Source: opensourc.es
Generate all possible configurations of colors. If yes then color it and otherwise try a different color. Such a graph is called as a Properly colored graph. If we consider the vertices 0 1 2 3 4 in left graph we can color the graph using 3 colors. Backtracking Set 5 m Coloring Problem-Backtracking-Given an undirected graph and a number m determine if the graph can be colored with at most m colors.
Source: slideplayer.com
Check if all vertices are colored or not. Step 3 Choose the next vertex and color it with the lowest numbered color that has not been colored on any vertices adjacent to it. Any connected simple planar graph with 5 or fewer vertices is 5colorable. This game is a variation of the Graph coloring problem where every cell denotes a node or vertex and there exists an edge between two nodes if the nodes are in the same row or. Steps To color graph using the Backtracking Algorithm.
Source: slidetodoc.com
We strongly recommend that you click here and practice it before moving on to the solution. Since each node can be coloured using any of the m available colours the total number of colour configurations possible are mV. Backtracking is undoubtedly quite simple - we explore each node as follows. Method to Color a Graph. This initialization is needed correct functioning of isSafe int color new intV.
Source: youtube.com
Step 1 Arrange the vertices of the graph in some order. Return false. If N is a goal node return success 2. Algorithm Algorithm solution for problem solved using BACKTRACKING are RECURSIVE The input to algorithm is vertex number present in the graph The algorithm generates the color number assigned to vertex and stores it an array. Method to Color a Graph.
Source: edward-huang.com
Backtracking Set 5 m Coloring Problem-Backtracking-Given an undirected graph and a number m determine if the graph can be colored with at most m colors. If all the adjacent vertices are colored with this color assign a new color. For solving the graph coloring problem we suppose that the graph is represented by its adjacency matrix G 1n 1n where G i j 1 if i j is an edge of G and Gi j 0 otherwise. Bool graphColoringUtilbool graphVV int m int color int v if v V return true. I if graphvi.
Source: dotnetpunch.wordpress.com
To explore node N. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color. If we consider the vertices 0 1 2 3 4 in left graph we can color the graph using 3 colors. Confirm whether it is valid to color the current vertex with the current color by checking whether any of its adjacent vertices are colored with the same color. Bed Threads Entire Collection 15 Skippable.
Source: dokumen.tips
Step 3 Choose the next vertex and color it with the lowest numbered color that has not been colored on any vertices adjacent to it. If N is a goal node return success 2. If the constraint are not matched at any point then remaining part of. Method to Color a Graph. Bool graphColoringUtilbool graphVV int m int color int v if v V return true.
Source: slidetodoc.com
Step 2 Choose the first vertex and color it with the first color. Bed Threads Entire Collection 15 Skippable. Graph coloring problem involves assigning colors to certain elements of a graph subject to certain restrictions and constraints. Graph Coloring Applications- Some important applications of graph coloring are as follows-Map Coloring. If N is a leaf node return failure 3.
Source: dokumen.tips
To explore node N. Backtracking is undoubtedly quite simple - we explore each node as follows. Steps To color graph using the Backtracking Algorithm. This has found applications in numerous fields in computer science. Graph Coloring Applications- Some important applications of graph coloring are as follows-Map Coloring.
Source: forns.lmu.build
Graph Coloring problem using backtracking- lecture55ADA - YouTube. If N is a goal node return success 2. If N is a leaf node return failure 3. Backtracking Set 5 m Coloring Problem-Backtracking-Given an undirected graph and a number m determine if the graph can be colored with at most m colors. Bool graphColoringbool graphVV int m int color.
Source:
Backtracking Set 5 m Coloring Problem-Backtracking-Given an undirected graph and a number m determine if the graph can be colored with at most m colors. I colori 0. The state- space tree for this above map is shown below. Call graphColoringUtil for vertex 0 if graphColoringUtilgraph m color 0 false printfSolution does not exist. This has found applications in numerous fields in computer science.
Source: slideshare.net
This initialization is needed correct functioning of isSafe int color new intV. Bool graphColoringUtilbool graphVV int m int color int v if v V return true. Steps To color graph using the Backtracking Algorithm. If we consider the vertices 0 1 2 3 4 in left graph we can color the graph using 3 colors. Graph Coloring problem using backtracking- lecture55ADA - YouTube.
Source:
Step 3 Choose the next vertex and color it with the lowest numbered color that has not been colored on any vertices adjacent to it. Therefore it is a properly colored graph. For solving the graph coloring problem we suppose that the graph is represented by its adjacency matrix G 1n 1n where G i j 1 if i j is an edge of G and Gi j 0 otherwise. Proof by induction on the number of vertices. A The principal states and territories of Australia.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring using backtracking example by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
