Your Graph coloring to sat images are ready in this website. Graph coloring to sat are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring to sat files here. Download all royalty-free photos and vectors.
If you’re searching for graph coloring to sat images information related to the graph coloring to sat topic, you have visit the right blog. Our website always gives you suggestions for refferencing the highest quality video and picture content, please kindly search and find more enlightening video articles and images that fit your interests.
Graph Coloring To Sat. To encode this as a SAT. 3-SAT P Graph 3-Coloring. It has been famously proven that all such 2D maps require a maximum of four colors. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
Planner Bundle Free Printables Planner Planner Bundle Planner Printables Free From pinterest.com
Graph to CNF Mapping. For every v 2V and every i 2f1kg introduce an atom p vi. 3-SAT P 3-Coloring Let x 1x nC 1C k be an instance of 3-SAT. This is called a vertex coloring. We show how to use 3-Coloring. Similarly an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color and a face coloring of a planar graph.
We will show that.
This is called a vertex coloring. All connected simple planar graphs are 5 colorable. If 3-SAT cant be solved in polynomial time then neither can 3-coloring. Intuitively this atom expresses that vertex v is assigned color i. Thus G can be partitioned into k independent sets i G is k-colorable. A python script is used to convert the graph to its SAT in CNF form which is then fed to a SAT solver zchaff which states whether the its colorable or not or simply undecidable.
Source: sandipanweb.wordpress.com
Proof by induction on the number of vertices. We follow a traditional encoding for graph coloring problems using SAT 10. B The graph coloring problem has a practical application in coloring maps. To 2-color a connected graph G pick an arbitrary node v and color it white Color all vs neighbors black Color all their uncolored neighbors white and so on If the algorithm terminates without a color conflict output the 2-coloring. Graph 2-Coloring can be decided in polynomial time.
Source: geeksforgeeks.org
For every v 2V and every i 2f1kg introduce an atom p vi. Similarly an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color and a face coloring of a planar graph. To prove this theorem we will take an instance of 3-SAT and turn it into an instance of 3-coloring. You need to add clauses to say that each vertex is blue or green or red namely i_rvee i_gvee i_b. T F B 31.
Source: pinterest.com
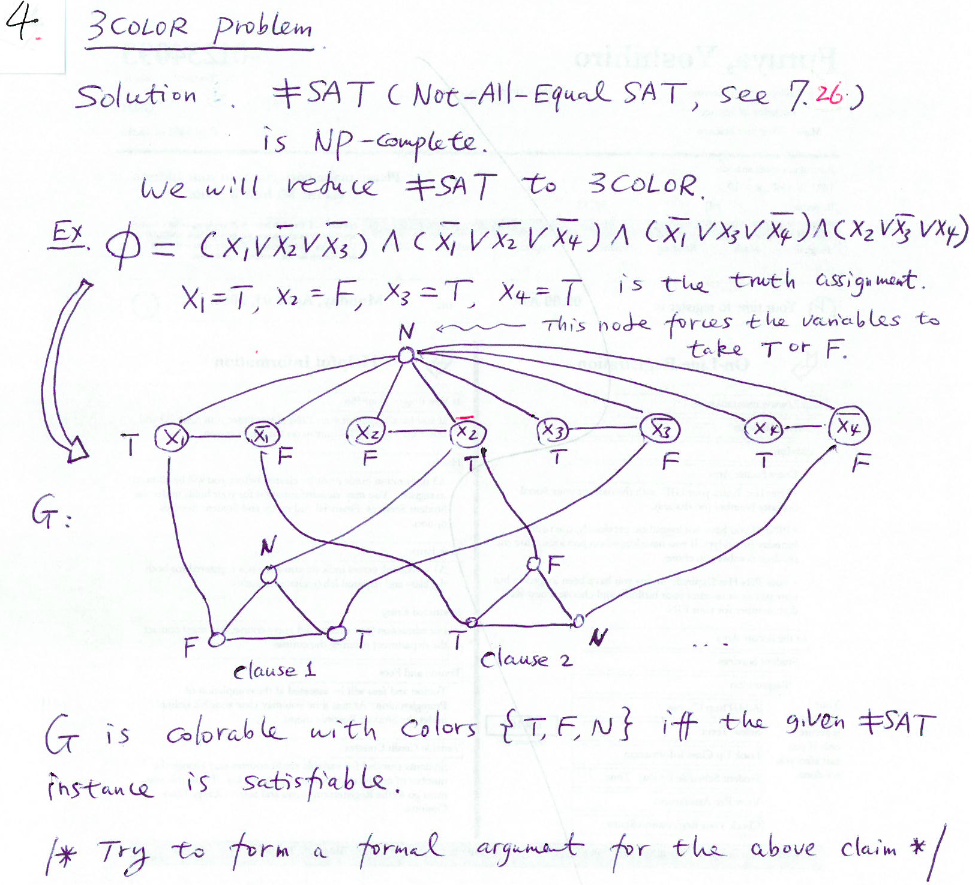
Some nodes on the input graph are pre-colored does not exist. For every variable x i create 2 nodes in G one for x i and one for x i. A valid coloring gives a certi cate. We follow a traditional encoding for graph coloring problems using SAT 10. That is we will show the following theorem.
Source: github.com
In our earlier formulation of reduction of k-colorable graph to 3-SAT 2 we generalized 1 for k-colorable graph. 3-SAT P 3-Coloring Let x 1x nC 1C k be an instance of 3-SAT. There is a linear time algorithm to. Some nodes on the input graph are pre-colored does not exist. Then it becomes a 3-SAT problem.
Source: quora.com
All connected simple planar graphs are 5 colorable. With your modeling setting i i_r i_g and i_b to false for all vertices yields a solution of the SAT problem and this is not a solution of the graph coloring problem. To construct the CNF phi we use. For this graph it can be achieved with three colors. A python script is used to convert the graph to its SAT in CNF form which is then fed to a SAT solver zchaff which states whether the its colorable or not or simply undecidable.
Source: uk.pinterest.com
Xi xi Create 3 special nodes T F and B joined in a triangle. Connect these nodes by an edge. We follow a traditional encoding for graph coloring problems using SAT 10. In this section we show how to encode the coloring of strips to SAT. If 3-SAT cant be solved in polynomial time then neither can 3-coloring.
Source: study.com
Xi xi Create 3 special nodes T F and B joined in a triangle. You need to add clauses to say that each vertex is blue or green or red namely i_rvee i_gvee i_b. Here each American state corresponds to a vertex and we add an edge if two states are adjacent. The standard graph generation reduction used in the previous section. We follow a traditional encoding for graph coloring problems using SAT 10.
Source: researchgate.net
The graph coloring problem aims to establish the smallest number of colors for which this is possible and return a satisfying assignment of colors. 3-SAT P Graph 3. All connected simple planar graphs are 5 colorable. Some nodes on the input graph are pre-colored does not exist. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
Source: chegg.com
To prove this theorem we will take an instance of 3-SAT and turn it into an instance of 3-coloring. To 2-color a connected graph G pick an arbitrary node v and color it white Color all vs neighbors black Color all their uncolored neighbors white and so on If the algorithm terminates without a color conflict output the 2-coloring. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. The graph coloring problem aims to establish the smallest number of colors for which this is possible and return a satisfying assignment of colors. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color.
Source: pinterest.com
Create graph Gφ such that Gφ is 3-colorable iff φ is satisfiable need to establish truth assignment for x1 x n via colors for some nodes in Gφ. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. Here each American state corresponds to a vertex and we add an edge if two states are adjacent. The graph coloring problem aims to establish the smallest number of colors for which this is possible and return a satisfying assignment of colors. To convert from 3-colorability to 3-SAT the constraints of graph coloring must be encoded in a Boolean formula.
Source: pinterest.com
Graph Coloring ObservationIf G is colored with k colors then each color class nodes of same color form an independent set in G. To reduce textsf 3-color to textsf SAT we transform the problem instance of textsf 3-color G langle V E rangle to the problem instance of textsf SAT phi in polynomial time. Connect these nodes by an edge. Some nodes on the input graph are pre-colored does not exist. But in this case it would only show that a specific 3-coloring ie.
Source: researchgate.net
The three colors used for the resulting 3-colorability problem will be red blue and green. However most proofs I have seen that reduce 3-SAT to 3-COLOR to prove that 3-SAT is NP-Complete use subgraph gadgets where some of the nodes are already colored. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. To convert from 3-colorability to 3-SAT the constraints of graph coloring must be encoded in a Boolean formula. For every v 2V and every i 2f1kg introduce an atom p vi.
Source: quora.com
Once we have proved this theorem we will know that. For this graph it can be achieved with three colors. 3-SAT P Graph 3. It doesnt show that no 3-coloring exists. A python script is used to convert the graph to its SAT in CNF form which is then fed to a SAT solver zchaff which states whether the its colorable or not or simply undecidable.
Source: pinterest.com
The standard graph generation reduction used in the previous section. For each shape s2Swe create k jKjvariables s 1s k. Let Sbe the set of shapes and K the set of colors. Approach from 3-Colorable graph to 3-SAT encoding. The standard graph generation reduction used in the previous section.
Source: es.pinterest.com
Any connected simple planar graph with 5 or fewer vertices is 5colorable. G is 2-colorable i G is bipartite. In graph theory graph coloring is a special case of graph labeling. Assume that there is a given graph G VE with V vertices and E edges. With your modeling setting i i_r i_g and i_b to false for all vertices yields a solution of the SAT problem and this is not a solution of the graph coloring problem.
Source: github.com
If 3-SAT cant be solved in polynomial time then neither can 3-coloring. G is 2-colorable i G is bipartite. Any connected simple planar graph with 5 or fewer vertices is 5colorable. To reduce textsf 3-color to textsf SAT we transform the problem instance of textsf 3-color G langle V E rangle to the problem instance of textsf SAT phi in polynomial time. To convert from 3-colorability to 3-SAT the constraints of graph coloring must be encoded in a Boolean formula.
Source: researchgate.net
Create triangle with node True False Base for each variable x i two nodes v i and v i connected in a. Two literals x_i and y_i to represent the color of. If 3-coloring can be solved in polynomial time then so can 3-SAT. In this section we show how to encode the coloring of strips to SAT. T F B 31.
Source: pinterest.com
To 2-color a connected graph G pick an arbitrary node v and color it white Color all vs neighbors black Color all their uncolored neighbors white and so on If the algorithm terminates without a color conflict output the 2-coloring. In our earlier formulation of reduction of k-colorable graph to 3-SAT 2 we generalized 1 for k-colorable graph. For each shape s2Swe create k jKjvariables s 1s k. Approach from 3-Colorable graph to 3-SAT encoding. B The graph coloring problem has a practical application in coloring maps.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring to sat by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
