Your Graph coloring register allocation images are ready in this website. Graph coloring register allocation are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring register allocation files here. Download all free vectors.
If you’re searching for graph coloring register allocation images information connected with to the graph coloring register allocation topic, you have pay a visit to the right site. Our website always gives you suggestions for downloading the maximum quality video and picture content, please kindly surf and find more informative video articles and images that match your interests.
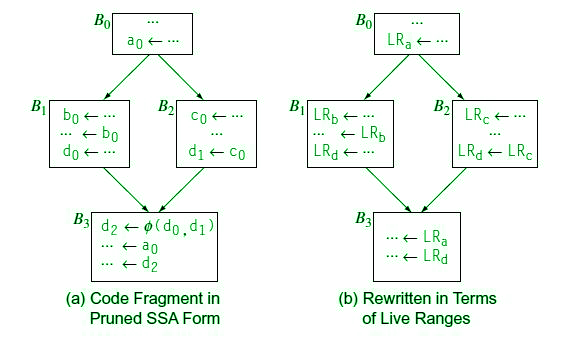
Graph Coloring Register Allocation. Nodes represent live range of the variable. Use graph coloring to model the allocation problem Build an interference graph Construct live ranges from examining program values Live ranges are nodes in the graph Edges between nodes indicate that they cannot share a physical register. For example global register allocation procedure. However it uses live ranges instead of live intervals.
Last Time Terminology Reminder W Simple Graph Vertex From slidetodoc.com
It is the allocators. Assign each object intermediate result name variable or constant to a distinct symbolic register. Register allocation is perhaps the single most important compiler optimization HP90. However it uses live ranges instead of live intervals. To model register allocation as a graph coloring problem the compiler first constructs an interference graph G. Use graph coloring to model the allocation problem Build an interference graph Construct live ranges from examining program values Live ranges are nodes in the graph Edges between nodes indicate that they cannot share a physical register.
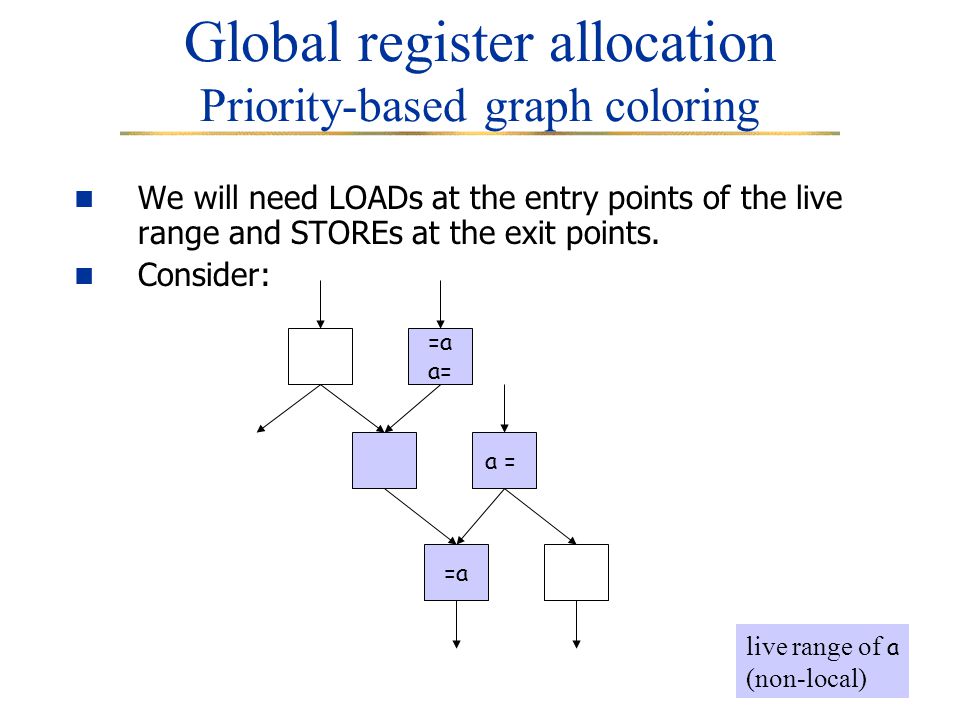
This addresses the problem mentioned above with linear scan allocation namely that if there are holes in a variables live interval then it can be wasteful to tie up a register for the entire live.
The predominant approach to analyzing variable lifetimes and allocating registers is through graph coloring. This paper advocates a decoupled. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively. Program values are represented by nodes in the interference graph and edges between nodes imply that those values cannot share a physical register. Allocation just inside a basic block is called Local Reg. Top-down approach and bottom-up approach.
Source: geeksforgeeks.org
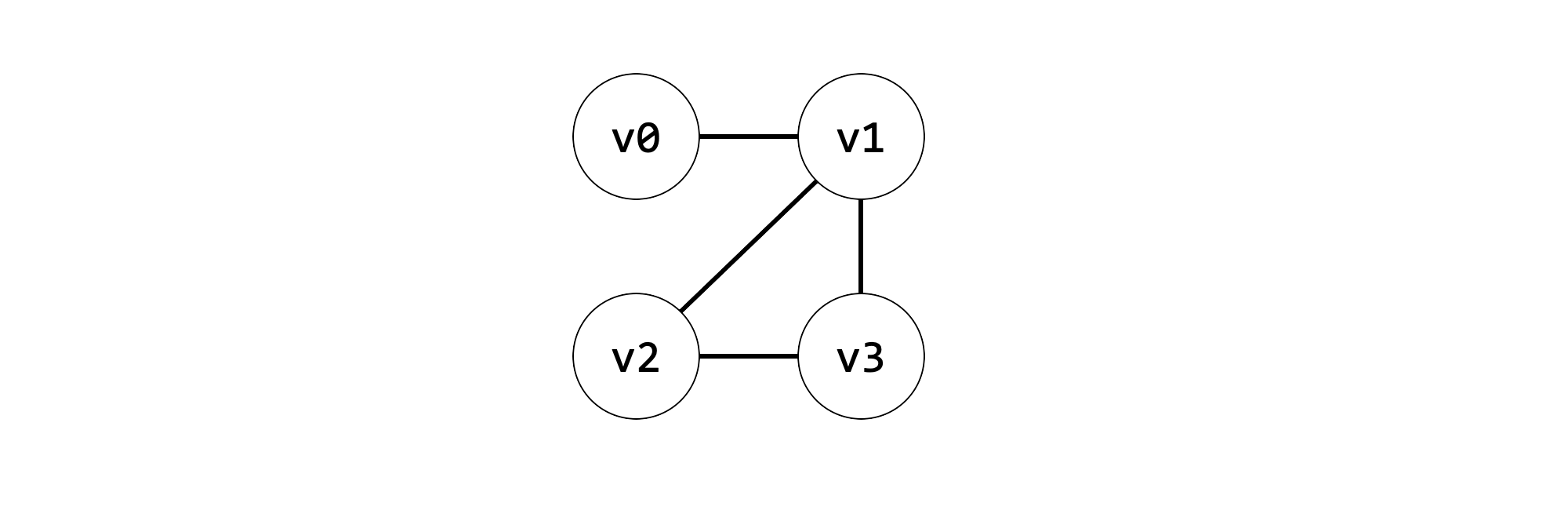
Edges represent the connection between two live ranges. The allocator discovers all of the separate live ranges and allocates them to physical registers on the target machine. Register allocation consists of the following main parts. A graph G vertices I. It is the allocators.
Source: pinterest.com
Edges represent the connection between two live ranges. 2 Graph Coloring Register Allocation Register allocatorstypically take an intermediate representation of a program as input. The allocator discovers all of the separate live ranges and allocates them to physical registers on the target machine. Values that cannot share a physical register are said to interfere with each other. Register allocation is perhaps the single most important compiler optimization HP90.
Source: slideshare.net
The colors used to color the graph represent registers. This paper advocates a decoupled. Our generalization permits simultaneous allocation of mul-tiple register classes even when registers alias while maintaining the efficiency and general structure of the original graph-coloring formulation. Graph coloring and linear scan are two appealing techniques for register allocation as the underlying formalism are ex-tremely clean and simple. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively.
Source:
2 Graph Coloring Register Allocation Register allocatorstypically take an intermediate representation of a program as input. Allocation just inside a basic block is called Local Reg. Graph coloring register allocators construct an interference graph that represents these safety constraints. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively. Two approaches for local reg.
Source:
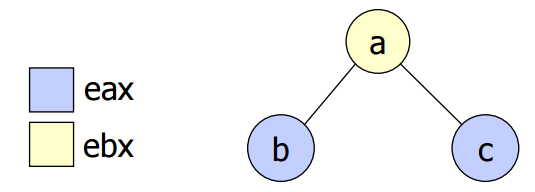
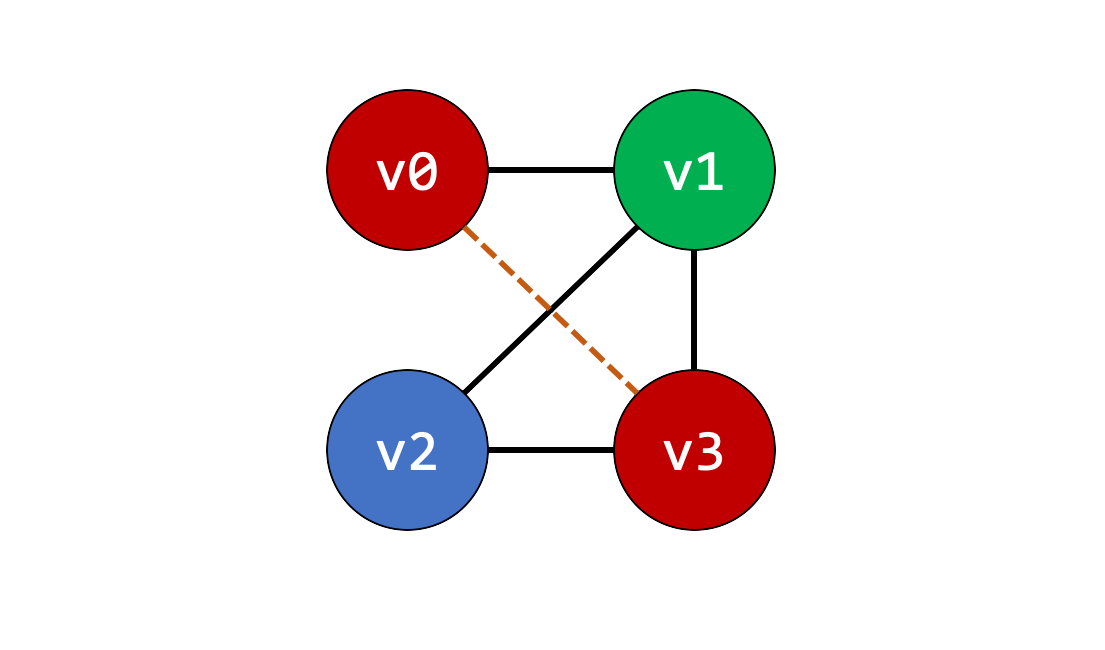
Allocation just inside a basic block is called Local Reg. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively. The nodes in G correspond to. To model register allocation as a graph coloring problem the compiler first constructs an interference graph G. Number of colors represents the minimum number of registers required.
Source: slideshare.net
Top-Down Approach is a simple approach based on Frequency Count. For example global register allocation procedure. The colors used to color the graph represent registers. Assign each object intermediate result name variable or constant to a distinct symbolic register. A graph G vertices I.
Source: slideshare.net
Register Allocation Through Graph Coloring In our problem colors registers We need to assign colors registers to graph nodes temporaries Let k number of machine registers If the RIG is k-colorable then there is a register assignment that uses no more than k registers. Register allocation is interpreted as a graph coloring problem. The process consists of creating a control flow graph computing alive variables at each point constructing interference graph and coloring graph. This representationdoesnot impose anyarchitecturallimitations onthe number of reg-isters values are contained in locations known as virtual registers. Values that cannot share a physical register are said to interfere with each other.
Source: pinterest.com
Register allocation is interpreted as a graph coloring problem. 2 Graph Coloring Register Allocation Register allocatorstypically take an intermediate representation of a program as input. For example global register allocation procedure. A graph G vertices I. Use graph coloring to model the allocation problem Build an interference graph Construct live ranges from examining program values Live ranges are nodes in the graph Edges between nodes indicate that they cannot share a physical register.
Source: geeksforgeeks.org
The nodes in G correspond to. Register allocation consists of the following main parts. For example global register allocation procedure. This graph is known as an interference graph. This paper advocates a decoupled.
Source: slideplayer.com
This graph is known as an interference graph. Despite the existence of reasonably good allocation algorithms the need for improved algorithms persists. Assign each object intermediate result name variable or constant to a distinct symbolic register. Register allocation is perhaps the single most important compiler optimization HP90. Keywordschromatic number interference graph graph coloring register allocation.
Source: slideplayer.com
Nodes represent live range of the variable. Values that cannot share a physical register are said to interfere with each other. An assignment can be produced in linear time using Interval-Graph Coloring. Program values are represented by nodes in the interference graph and edges between nodes imply that those values cannot share a physical register. Graph coloring register allocators construct an interference graph that represents these safety constraints.
Source: slidetodoc.com
For example global register allocation procedure. Assign each object intermediate result name variable or constant to a distinct symbolic register. Use graph coloring to model the allocation problem Build an interference graph Construct live ranges from examining program values Live ranges are nodes in the graph Edges between nodes indicate that they cannot share a physical register. In this approach nodes in the graph represent variables and edges represent live range conflicts. The graph-coloring metaphor leads to elegant algorithms for register allocation that have been shown to be quite effective for regular architectures with plenty of registers.
Source: easyexamnotes.com
Number of colors represents the minimum number of registers required. Nodes represent live range of the variable. A graph G vertices I. The colors used to color the graph represent registers. Assign each object intermediate result name variable or constant to a distinct symbolic register.
Source: geeksforgeeks.org
This addresses the problem mentioned above with linear scan allocation namely that if there are holes in a variables live interval then it can be wasteful to tie up a register for the entire live. The colors used to color the graph represent registers. An assignment can be produced in linear time using Interval-Graph Coloring. This representationdoesnot impose anyarchitecturallimitations onthe number of reg-isters values are contained in locations known as virtual registers. Each color represents a.
Source: chrisseaton.com
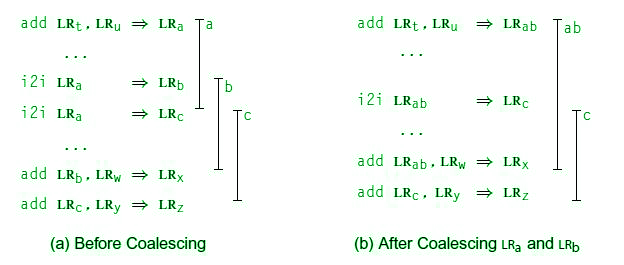
Usedef chaining plus getting the right number of names building the interference graph coalescing nodes attempting to find a 32-coloring of the graph and if one cannot be found modifying the program and its graph until a 32-coloring is obtained. A k-coloring of the graph is mapped to k registers. Use graph coloring to model the allocation problem Build an interference graph Construct live ranges from examining program values Live ranges are nodes in the graph Edges between nodes indicate that they cannot share a physical register. Each color represents a. Register allocation is perhaps the single most important compiler optimization HP90.
Source: chrisseaton.com
This representationdoesnot impose anyarchitecturallimitations onthe number of reg-isters values are contained in locations known as virtual registers. Top-Down Approach is a simple approach based on Frequency Count. Edges represent the connection between two live ranges. The colors used to color the graph represent registers. This addresses the problem mentioned above with linear scan allocation namely that if there are holes in a variables live interval then it can be wasteful to tie up a register for the entire live.
Source: youtube.com
Nodes represent live range of the variable. Program values are represented by nodes in the interference graph and edges between nodes imply that those values cannot share a physical register. Each color represents a. Usedef chaining plus getting the right number of names building the interference graph coalescing nodes attempting to find a 32-coloring of the graph and if one cannot be found modifying the program and its graph until a 32-coloring is obtained. Graph coloring and linear scan are two appealing techniques for register allocation as the underlying formalism are ex-tremely clean and simple.
Source: sites.google.com
Graph Coloring Register Allocation Effective approach. Register Allocation via Graph Coloring The basic idea behind register allocation via graph coloring is to reduce register spillage by globally assigning variables to registers across an entire program module via the five basic steps below. A graph G vertices I. Assigning color to the nodes such that no two adjacent nodes have same color. This paper generalizes the graph-coloring approach to register allocation in a way that eliminates the need for the kinds of workarounds currently employed formodern commercial architec-tures.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring register allocation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
