Your Graph coloring problems their applications scheduling images are ready. Graph coloring problems their applications scheduling are a topic that is being searched for and liked by netizens now. You can Get the Graph coloring problems their applications scheduling files here. Get all free vectors.
If you’re looking for graph coloring problems their applications scheduling images information connected with to the graph coloring problems their applications scheduling keyword, you have come to the ideal site. Our website always gives you hints for downloading the maximum quality video and image content, please kindly surf and find more informative video content and images that fit your interests.
Graph Coloring Problems Their Applications Scheduling. Indeed for any given integers k l there are graphs with clique number k and chromatic number l. You will be redirected to the full text document in the repository in a few seconds if not click hereclick here. G RAPH COLORING PROBLEMS AND THEIR APPLICATIONS IN SCHEDULING D ANIEL M ARX Department of Computer Science and Information Theory Budapest University of Technology and Economics H-1521 Budapest Hungary dmarxcsbmehu Abstract Graph coloring and its generalizations are useful tools in modeling a wide variety of scheduling and assignment problems. The sudoku is then a graph of 81 vertices and chromatic number 9.
Machine Learning Bubble Chart Machine Learning Bubble Chart Data Science From pinterest.com
Applications On Graph Theory. Graph colouring and its generalizations are useful tools in modelling a wide variety of scheduling and assignment problems. Sudoku is one of the most interested number placement-puzzle and it is also a variation of Graph-coloring problem. Indeed for any given integers k l there are graphs with clique number k and chromatic number l. The problem is to assign the courses a given number of time slots colors where each time slot can be used for a given number of class rooms. This approach separates the area to more than parts.
All connected simple planar graphs are 5 colorable.
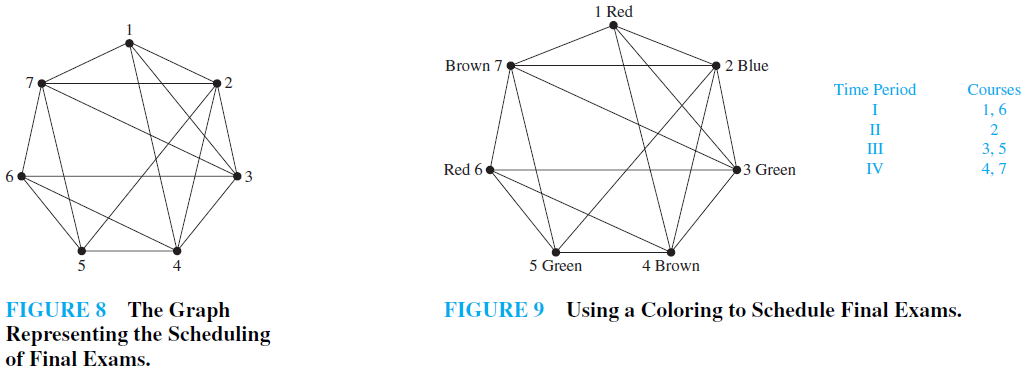
A graph G is k-chromatic if χGk. Quite a few practical problems in scheduling can be expressed as a problem in graph coloring. The exam-scheduling problem as explained above imposes a constraint on The coloring scheme for the exam-scheduling problem the maximum number of nodes assigned the same uses a double indexed color RIJ where the index I color. Map coloring is a type of problem that can be solved by using graph coloring approach. In this paper we review several variants of graph colouring such as precolouring extension list colouring multicolouring minimum sum colouring and discuss their applications in scheduling. Optimal colouring of G is a χG-colouring.
Source: pinterest.com
1 Making Schedule or Time Table. Indeed for any given integers k l there are graphs with clique number k and chromatic number l. Graph coloring and its generalizations are useful tools in modeling a wide variety of scheduling and assignment problems. Any connected simple planar graph with 5 or fewer vertices is 5colorable. This method is used in time tabling problem in 1967 by Welsh and Powel 8.
Source: cz.pinterest.com
Solutions to graph colouring problems have wide applicability including in aircraft scheduling organising file transfer between processors and radio frequency assignments 31. In this paper we review several variants of graph colouring such as precolouring extension list colouring multicolouring minimum sum colouring and discuss their applications in scheduling. This approach separates the area to more than parts. The problem is to assign the courses a given number of time slots colors where each time slot can be used for a given number of class rooms. The Graph Coloring Problem GCP can be simply defined as partitioning the vertices of a graph into independent sets while minimizing the number of colors used.
Source: pinterest.com
1 Making Schedule or Time Table. Suppose we want to make am exam schedule for a university. The graph coloring problem has huge number of applications. Any connected simple planar graph with 5 or fewer vertices is 5colorable. Sudoku can be seen as a graph coloring problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge.
Source: researchgate.net
All connected simple planar graphs are 5 colorable. This paper is concerned with the problem of course timetable scheduling where graph coloring can provide an algorithm 9 which will prevent or at least minimize conflicting schedules. Each node represents exams and the edge between nodes. In this paper we review several variants of graph colouring such as precolouring extension list colouring multicolouring minimum sum colouring and discuss their applications in scheduling. 12 2003 Abstract Graph colouring and its generalizations are useful tools in modelling a wide variety of scheduling and assignment problems.
Source: pinterest.com
Thus optimal solutions to such problems may. Solutions to graph colouring problems have wide applicability including in aircraft scheduling organising file transfer between processors and radio frequency assignments 31. The graph multi-coloring problem is an extension of the. The graph coloring problem has huge number of applications. Sudoku is one of the most interested number placement-puzzle and it is also a variation of Graph-coloring problem.
Source: youtube.com
In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling. Optimal colouring of G is a χG-colouring. So far many approaches have been. All connected simple planar graphs are 5 colorable. The graph coloring problem GCP consists of assigning a single color integer to each vertex of an undirected graph such that no two adjacent vertices share the same color with the objective of minimizing the number of colors.
Source: pinterest.com
The graph multi-coloring problem is an extension of the. Graph coloring and its generalizations are useful tools in modeling a wide variety of scheduling and assignment problems. The graph coloring problem has huge number of applications. Applications of Graph Coloring Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling.
Source: mdpi.com
Obviously the complete graph Kn requires n colours so χKnn. The Graph Coloring Problem GCP can be simply defined as partitioning the vertices of a graph into independent sets while minimizing the number of colors used. Wood 1969 and Welsh and Powell 1967 have pointed out the connection between the basic examination scheduling problem and the problem of coloring the vertices of a graph using the minimum number of colors such that no two adjacent vertices have the same color. The graph multi-coloring problem is an extension of the. Proof by induction on the number of vertices.
Source: fr.pinterest.com
This method is used in time tabling problem in 1967 by Welsh and Powel 8. Wood 1969 and Welsh and Powell 1967 have pointed out the connection between the basic examination scheduling problem and the problem of coloring the vertices of a graph using the minimum number of colors such that no two adjacent vertices have the same color. In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling. Indeed for any given integers k l there are graphs with clique number k and chromatic number l. Applications of Graph Coloring Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints.
Source: pinterest.com
So far many approaches have been. This bound can be tight but it can also be very loose. Indeed for any given integers k l there are graphs with clique number k and chromatic number l. This method is used in time tabling problem in 1967 by Welsh and Powel 8. Without coloring the two adjacent parts to same color all map is colored.
Source: skedsoft.com
The sudoku is then a graph of 81 vertices and chromatic number 9. The graph coloring problem has huge number of applications. You will be redirected to the full text document in the repository in a few seconds if not click hereclick here. So far many approaches have been. GRAPH COLOURING PROBLEMS AND THEIR APPLICATIONS IN SCHEDULING Dániel MARX Department of Computer Science and Information Theory Budapest University of Technology and Economics H1521 Budapest Hungary e-mail.
Source: pinterest.com
The sudoku is then a graph of 81 vertices and chromatic number 9. GRAPH COLOURING PROBLEMS AND THEIR APPLICATIONS IN SCHEDULING Dániel MARX Department of Computer Science and Information Theory Budapest University of Technology and Economics H1521 Budapest Hungary e-mail. Obviously the complete graph Kn requires n colours so χKnn. Sudoku is one of the most interested number placement-puzzle and it is also a variation of Graph-coloring problem. The problem is to assign the courses a given number of time slots colors where each time slot can be used for a given number of class rooms.
Source: pinterest.com
In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling. Thus optimal solutions to such problems may. This paper is concerned with the problem of course timetable scheduling where graph coloring can provide an algorithm 9 which will prevent or at least minimize conflicting schedules. The graph coloring problem GCP consists of assigning a single color integer to each vertex of an undirected graph such that no two adjacent vertices share the same color with the objective of minimizing the number of colors. So far many approaches have been.
Source: semanticscholar.org
This method is used in time tabling problem in 1967 by Welsh and Powel 8. 12 2003 Abstract Graph colouring and its generalizations are useful tools in modelling a wide variety of scheduling and assignment problems. Suppose we want to make am exam schedule for a university. The graph coloring problem GCP consists of assigning a single color integer to each vertex of an undirected graph such that no two adjacent vertices share the same color with the objective of minimizing the number of colors. So far many approaches have been.
Source: pinterest.com
Thus optimal solutions to such problems may. A graph G is k-chromatic if χGk. Map coloring is a type of problem that can be solved by using graph coloring approach. You will be redirected to the full text document in the repository in a few seconds if not click hereclick here. The Graph Coloring Problem GCP can be simply defined as partitioning the vertices of a graph into independent sets while minimizing the number of colors used.
Source: pinterest.com
Thus optimal solutions to such problems may. The graph multi-coloring problem is an extension of the. In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling. In this paper we review several variants of graph coloring such as precoloring extension list coloring multicoloring minimum sum coloring and discuss their applications in scheduling. The Graph Coloring Problem GCP can be simply defined as partitioning the vertices of a graph into independent sets while minimizing the number of colors used.
Source: pinterest.com
Sudoku is one of the most interested number placement-puzzle and it is also a variation of Graph-coloring problem. Sudoku can be seen as a graph coloring problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge. GRAPH COLOURING PROBLEMS AND THEIR APPLICATIONS IN SCHEDULING Dániel MARX Department of Computer Science and Information Theory Budapest University of Technology and Economics H1521 Budapest Hungary e-mail. Here some problems that can be solved by concepts of graph coloring methodologies. 12 2003 Abstract Graph colouring and its generalizations are useful tools in modelling a wide variety of scheduling and assignment problems.
Source: pinterest.com
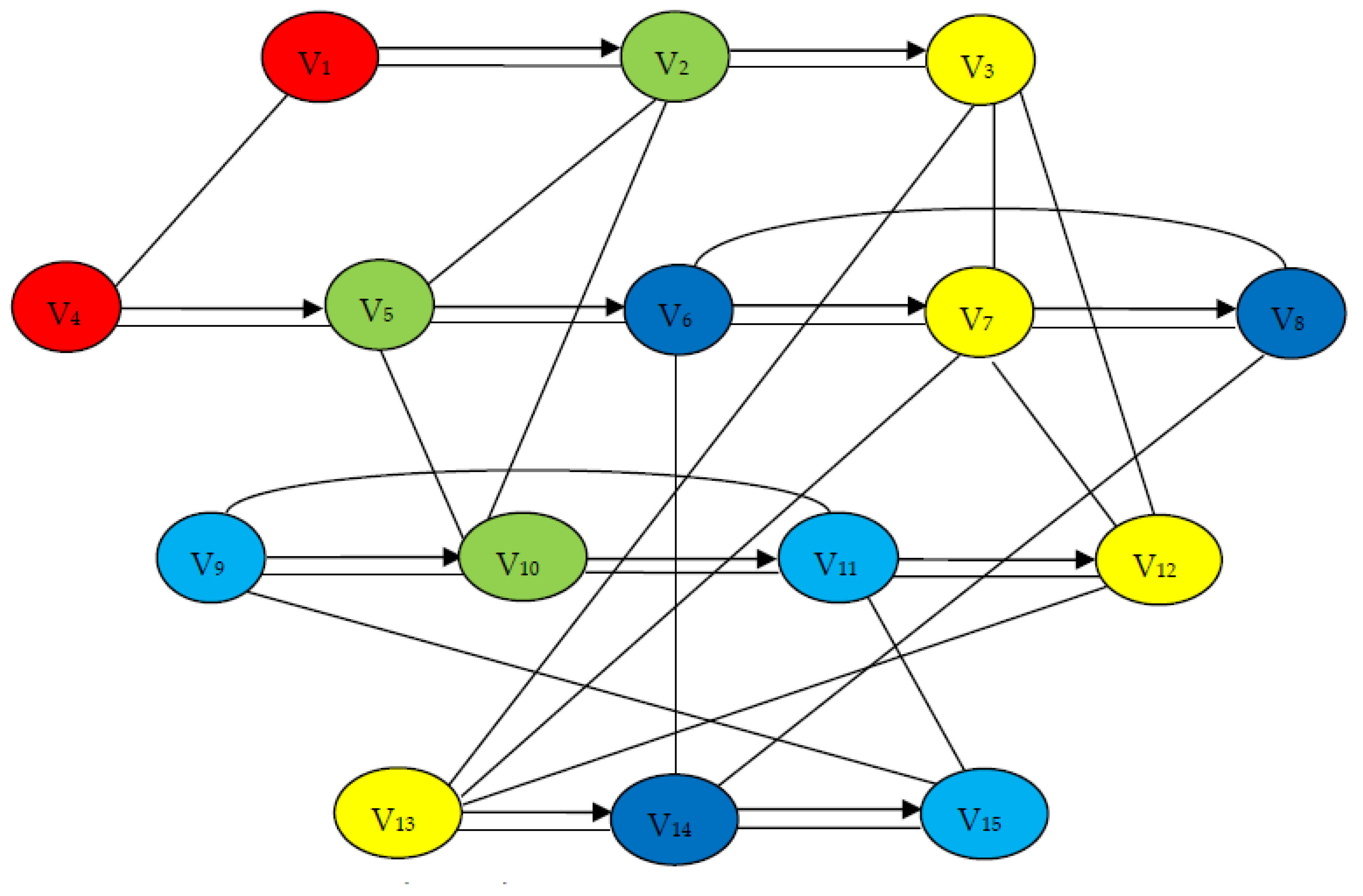
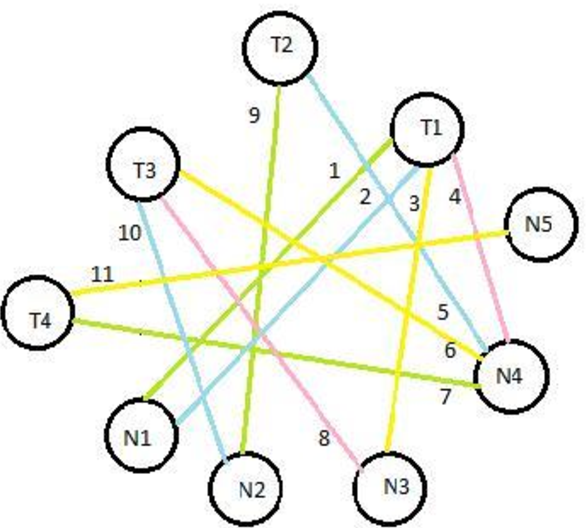
The class scheduling problem can be modeled by a graph where the vertices and edges represent the courses and the common students respectively. Graph colouring and its generalizations are useful tools in modelling a wide variety of scheduling and assignment problems. The graph coloring problem GCP consists of assigning a single color integer to each vertex of an undirected graph such that no two adjacent vertices share the same color with the objective of minimizing the number of colors. Proof by induction on the number of vertices. Any connected simple planar graph with 5 or fewer vertices is 5colorable.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring problems their applications scheduling by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
