Your Graph coloring open problems images are available in this site. Graph coloring open problems are a topic that is being searched for and liked by netizens today. You can Find and Download the Graph coloring open problems files here. Find and Download all free photos and vectors.
If you’re searching for graph coloring open problems images information connected with to the graph coloring open problems topic, you have pay a visit to the ideal site. Our site frequently provides you with hints for refferencing the highest quality video and image content, please kindly hunt and find more enlightening video articles and graphics that match your interests.
Graph Coloring Open Problems. The two problems below can be solved using graph coloring. Then M must be the same color as H since M is adjacent to G and L and there are only three colors available. V 1k such that ri rj for each edge ij E. All right and then the minimum number of colors you need is called the chromatic number of the graph.
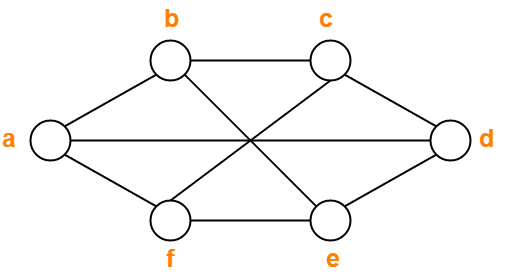How To Find Chromatic Number Graph Coloring Algorithm Gate Vidyalay From gatevidyalay.com
We introduce a new variation to list coloring which we call choosability with union separation. In page 104 section 512 the following problem is stated as the Erdos-Lovasz Tihany Problem. Then M must be the same color as H since M is adjacent to G and L and there are only three colors available. We start by coloring G H and L three di erent colors as we must. CoRE 414 Emailhochbergdimacsrutgersedu DESCRIPTION. A survey of Hadwigers Conjecture Section 13.
For each problem represent the situation with a graph say whether you should be coloring vertices or edges and why and use the coloring to solve the problem.
Our results show that the model which achieves high accuracy upon training on random instances is able to generalise to graph distributions different from those seen at training time. Hadwigers Conjecture for k4 was first proved by Hadwiger in 1943. Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. The two problems below can be solved using graph coloring. For each problem represent the situation with a graph say whether you should be coloring vertices or edges and why and use the coloring to solve the problem. A survey of Hadwigers Conjecture Section 13.
Source: adam-rumpf.github.io
Given a graph GVE find a minimum k and a mapping r. All right and then the minimum number of colors you need is called the chromatic number of the graph. Unit Distance Graphs—chromatic number RESEARCHER. Your Quidditch league has 5 teams. The book has ISBN number 0-471-02865-7.
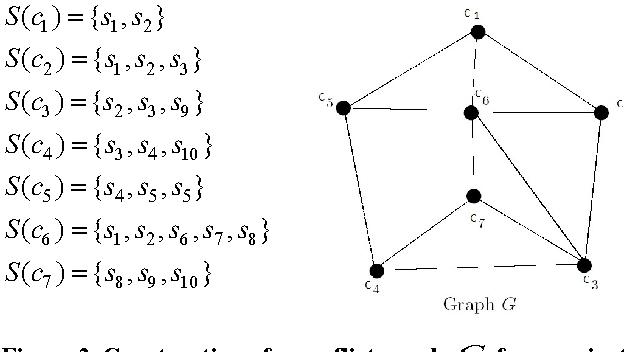
Source: researchgate.net
In page 104 section 512 the following problem is stated as the Erdos-Lovasz Tihany Problem. Then M must be the same color as H since M is adjacent to G and L and there are only three colors available. We might as well assume they are the colors as shown above. Given a graph GVE find a minimum k and a mapping r. Jensen and Bjarne Toft Wiley Interscience 1995 dedicated to Paul Erdős.
Source: semanticscholar.org
We give brief descriptions of the problems we study here. Following is the basic Greedy Algorithm to assign colors. Graph coloring problem is to assign colors to certain elements of a graph subject to certain constraints. The two-coloring of the vertices of the bipartite graph induces a two-coloring of the edges of G such that the two edges of any induced P 3 in G have distinct colors. Geographical maps of countries or states where no two adjacent cities cannot be assigned same color.
Source: gatevidyalay.com
Your Quidditch league has 5 teams. But later our professor found an alternative statement of the problem in the book named GRAPH COLORING PROBLEMS by Jensen and Toft. Vertex coloring is the most common graph coloring problem. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. The two-coloring of the vertices of the bipartite graph induces a two-coloring of the edges of G such that the two edges of any induced P 3 in G have distinct colors.
Source: researchgate.net
As discussed in the previous post graph coloring is widely used. All right and then the minimum number of colors you need is called the chromatic number of the graph. For a graph G a list assignment Lto the vertices of Gis a kk t-list assignment if every. We can check if a graph is Bipartite or not by coloring the graph using two colors. The original list price was US 4495.
Source: ics.uci.edu
Vertex Degrees and Colorings. We consider two branches of coloring problems for graphs. The book has ISBN number 0-471-02865-7. Planar graphs to solve the famous four color problem. Unit Distance Graphs—chromatic number RESEARCHER.
Source: wikiwand.com
Graph Coloring Problems Here are the archives for the book Graph Coloring Problems by Tommy R. In this work we showcase how Graph Neural Networks GNN can be engineered – with a very simple architecture – to solve the fundamental combinatorial problem of graph colouring. The problem is given m colors find a way of coloring the vertices of a graph such that no. In page 104 section 512 the following problem is stated as the Erdos-Lovasz Tihany Problem. How many colors are needed so that if each point in the plane is assigned one of the colors no two points which are exactly distance 1 apart will be assigned the same color.
Source: semanticscholar.org
Your Quidditch league has 5 teams. This is the classical problem when each node in the graph is assigned one color and colors for adjacent nodes must be different. In a coloring game two players use a given set of colors to construct a coloring of a graph following specific rules depending on the game we consider. The problem is given m colors find a way of coloring the vertices of a graph such that no. Following is the basic Greedy Algorithm to assign colors.
Source: ics.uci.edu
This problem has been open since 1956. Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. Geographical maps of countries or states where no two adjacent cities cannot be assigned same color. How many colors are needed so that if each point in the plane is assigned one of the colors no two points which are exactly distance 1 apart will be assigned the same color. We can check if a graph is Bipartite or not by coloring the graph using two colors.
Source: wikiwand.com
Then M must be the same color as H since M is adjacent to G and L and there are only three colors available. There are approximate algorithms to solve the problem though. We start by coloring G H and L three di erent colors as we must. Coloring problems in graph theory Created Date. The two-coloring of the vertices of the bipartite graph induces a two-coloring of the edges of G such that the two edges of any induced P 3 in G have distinct colors.
Source: medium.com
CoRE 414 Emailhochbergdimacsrutgersedu DESCRIPTION. The original list price was US 4495. Four colors are sufficient to color. Then M must be the same color as H since M is adjacent to G and L and there are only three colors available. See this for more details.
Source: gatevidyalay.com
Your Quidditch league has 5 teams. Planar graphs to solve the famous four color problem. This can be done by giving each of these vertices. Jensen and Bjarne Toft Wiley Interscience 1995 dedicated to Paul Erdős. You will play a tournament next week in which every team will play every other team once.
Source: wikiwand.com
This can be done by giving each of these vertices. Given a graph GVE find a minimum k and a mapping r. The problem is given m colors find a way of coloring the vertices of a graph such that no. The two problems below can be solved using graph coloring. 21 The Graph Coloring Problem Problem.
Source: researchgate.net
We consider two branches of coloring problems for graphs. We introduce a new variation to list coloring which we call choosability with union separation. For each problem represent the situation with a graph say whether you should be coloring vertices or edges and why and use the coloring to solve the problem. So the minimum value of K for which such a coloring exist is the chromatic number OF the graph. CoRE 414 Emailhochbergdimacsrutgersedu DESCRIPTION.
Source: medium.com
Coloring game problems arose as game-theoretic versions of well-known graph coloring problems. The two-coloring of the vertices of the bipartite graph induces a two-coloring of the edges of G such that the two edges of any induced P 3 in G have distinct colors. Jensen and Bjarne Toft Wiley Interscience 1995 dedicated to Paul Erdős. See this for more details. The book has ISBN number 0-471-02865-7.
Source: wikiwand.com
But later our professor found an alternative statement of the problem in the book named GRAPH COLORING PROBLEMS by Jensen and Toft. List coloring and packing coloring. There are approximate algorithms to solve the problem though. You will play a tournament next week in which every team will play every other team once. Planar graphs to solve the famous four color problem.
Source: towardsdatascience.com
Graph Coloring Problems Here are the archives for the book Graph Coloring Problems by Tommy R. In page 104 section 512 the following problem is stated as the Erdos-Lovasz Tihany Problem. Given a graph GVE find a minimum k and a mapping r. All right and then the minimum number of colors you need is called the chromatic number of the graph. There are approximate algorithms to solve the problem though.
Source: semanticscholar.org
Our results show that the model which achieves high accuracy upon training on random instances is able to generalise to graph distributions different from those seen at training time. Unit Distance Graphs—chromatic number RESEARCHER. List coloring and packing coloring. Sudoku can be seen as a graph coloring problem where the squares of the grid are vertices and the numbers are colors that must be different if in the same row column or 3 3 3 times 3 3 3 grid such vertices in the graph are connected by an edge. In this work we showcase how Graph Neural Networks GNN can be engineered – with a very simple architecture – to solve the fundamental combinatorial problem of graph colouring.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring open problems by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
