Your Graph coloring np hard images are available in this site. Graph coloring np hard are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring np hard files here. Find and Download all royalty-free images.
If you’re looking for graph coloring np hard pictures information connected with to the graph coloring np hard keyword, you have come to the right blog. Our site frequently provides you with hints for downloading the highest quality video and picture content, please kindly search and locate more informative video content and images that fit your interests.
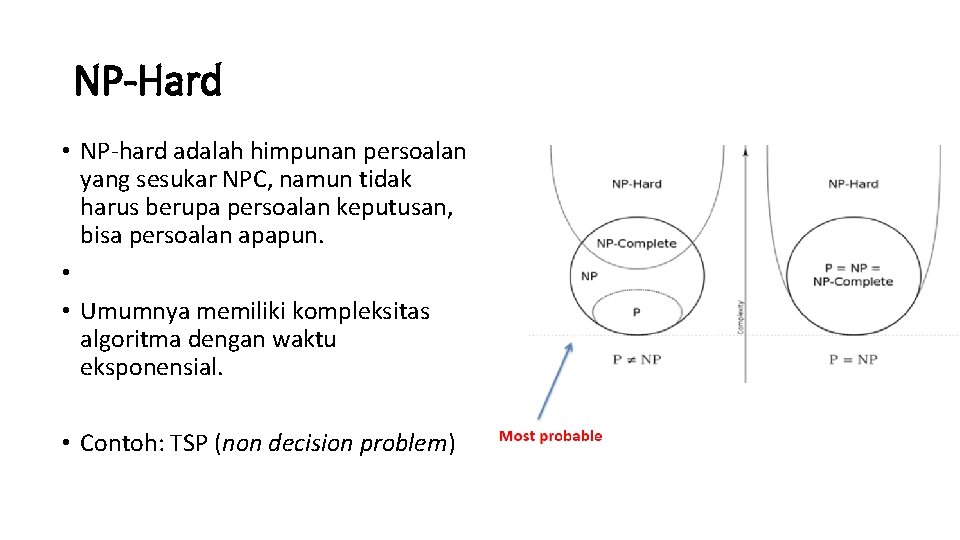
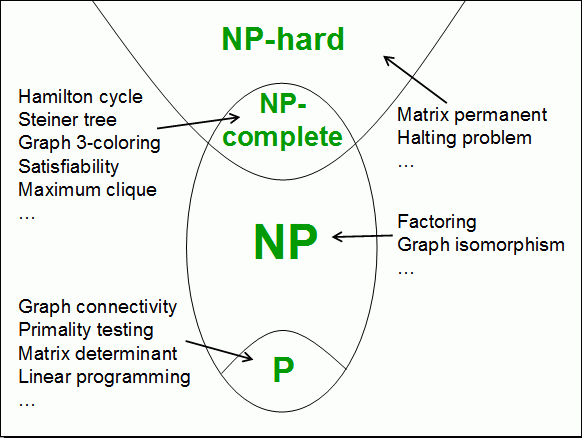
Graph Coloring Np Hard. N via colors for some nodes in Gφ. Given a graph G can you color the nodes with k colors such that the endpoints of every edge are colored di erently. This highlights a qualitative difference between the known hardness result for coloring 3-colorable graphs and the factor nε hardness for approximating the chromatic. The problem to find chromatic number of a given graph is NP Complete.
Summary Nphard And Npcompleteness Proof Polynomial Time Reduction From slidetodoc.com
We give a polynomial-time reduction from 3-COLOR to 4-COLOR. A k-coloring is a function f. Applications of Graph Coloring. So f is a polytime many-one reduction from an NP-hard problem K-COLORING to MIN-MONOCHROMATIC so we conclude that the latter is NP-hard. N via colors for some nodes in Gφ. The degeneracy of G denoted δG is the smallest k such that G is k-degenerate.
Check out the course here.
Graph coloring is one such heuristic algorithm that can deal timetable scheduling satisfying changing requirements evolving subject demands and. I have seen papers that show vertex coloring for a k-unoform hypergraph is NP-hard. The degeneracy of G denoted δG is the smallest k such that G is k-degenerate. Step 2 Choose the first vertex and color it with the first color. A graph G is k-degenerate if each of its subgraphs has a vertex of degree at most k. Suppose we want to make am exam schedule for a university.
Source: slidetodoc.com
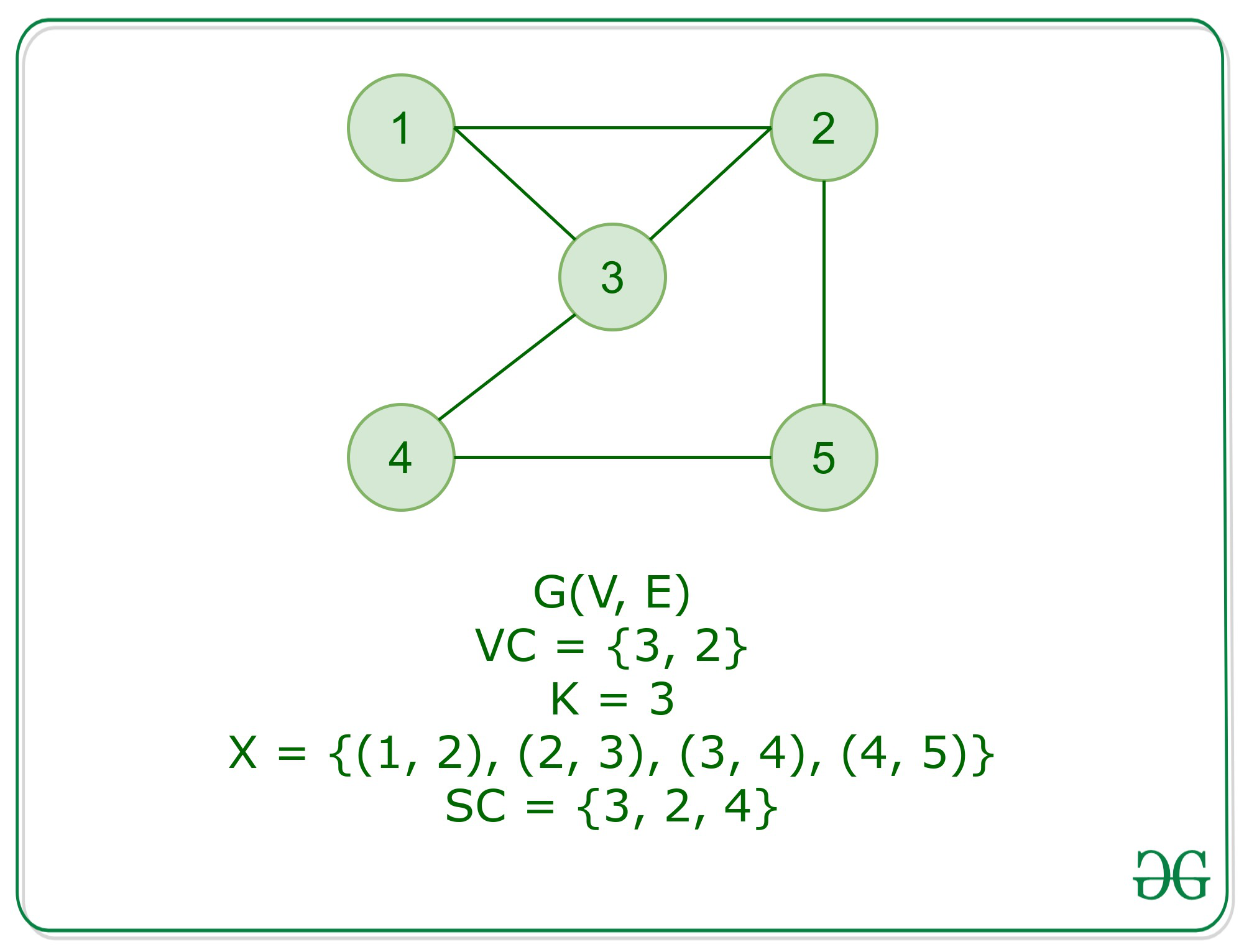
We have list different subjects and students enrolled in every subject. A graph G is k-degenerate if each of its subgraphs has a vertex of degree at most k. We show that obtaining the lexicographically rst four coloring of a planar graph is NPhard. Corresponding optimization problem is NP Hard. The problem of coloring a graph with the minimum number of colors is well known to be NP-hard even restricted to k-colorable graphs for constant k 3.
Source: vips3201v.medium.com
The problem of coloring a graph with the minimum number of colors is well known to be NP-hard even restricted to k-colorable graphs for constant k 3. The graph coloring problem has huge number of applications. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be. We have list different subjects and students enrolled in every subject. Is vertex coloring of a hypergraph with no uniformity restriction NP-hard.
Source:
Interpret this as a truth assignment to v i For each clause C j abc create a small gadget graph. In order to prove that the 3-coloring problem is NP-Hard perform a reduction from a known NP-Hard problem to this problem. Check out the course here. This type of NP-Hard problem can be efficiently solved using graph coloring when compared to general graphs. Garey and Johnson 10 proved that it is NP-hard to approximate the chromatic number within a factor of 2 for any 0The best known algorithm for general graphs appears in 13 and colors a graph using a number of.
Source: quora.com
We show that obtaining the lexicographically rst four coloring of a planar graph is NPhard. We have list different subjects and students enrolled in every subject. This shows that planar graph four-coloring is not self-reducible assuming P6 NP. For each edge u v in graph G verify that the color cu cv Hence the assignment can be checked for correctness in the polynomial-time of the graph with respect to its edges OVE. Graph coloring problem is a NP Complete problem.
Source: geeksforgeeks.org
Corresponding optimization problem is NP Hard. Create triangle with node True False Base for each variable x i two nodes v i and v i connected in a triangle with common Base If graph is 3-colored either v i or v i gets the same color as True. This video is part of an online course Intro to Algorithms. The degeneracy of G denoted δG is the smallest k such that G is k-degenerate. This problem can be described as an np hard problem it means it cannot be solved in polynomial time algorithm.
Source: baeldung.com
If all the adjacent vertices are colored with this color. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be. I have seen papers that show vertex coloring for a k-unoform hypergraph is NP-hard. We show that obtaining the lexicographically rst four coloring of a planar graph is NPhard. Also clearly f can be computed in polynomial time.
Source: slideplayer.info
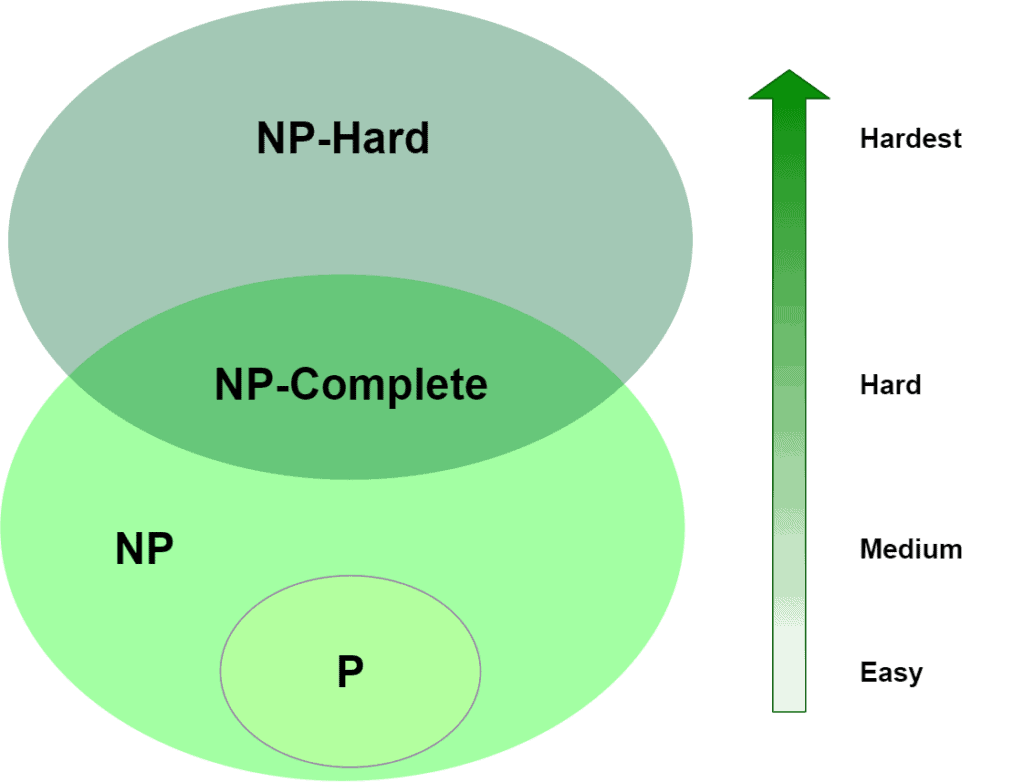
Given a graph G can you color the nodes with k colors such that the endpoints of every edge are colored di erently. A k-coloring is a function f. This shows that planar graph four-coloring is not self-reducible assuming P6 NP. The bound G1 may be lowered by finding orderings yielding a greedy colouring with less than G1 colours. NP-Complete NP-Hard If you can show that a problem is equivalent can be reduced to a known NP-Complete problem you may as well not try to find an efficient solution for it unless youre convinced youre a genius If such a polynomial solution exists P NP It is not known whether P NP or P NP.
Source: slidetodoc.com
Step 1 Arrange the vertices of the graph in some order. Graph coloring problem is a NP Complete problem. 1 Making Schedule or Time Table. So f is a polytime many-one reduction from an NP-hard problem K-COLORING to MIN-MONOCHROMATIC so we conclude that the latter is NP-hard. The definition of coloring implies that GK is in K-COLORING iff Gk0 is in MIN-MONOCHROMATIC.
Source: researchgate.net
We give a polynomial-time reduction from 3-COLOR to 4-COLOR. The Graph Coloring decision problem is np-complete ie asking for existence of a coloring with less than q colors as given a coloring it can be easily checked in polynomial time whether or not it uses less than q colors. The reduction maps a graph ji into a new graph such that k 3-COLOR if and only if i 4-COLOR. This paper explores the approximation problem of coloring k-colorable graphs with as few additional colors as possible in polynomial time with special focus on the case of k 3. NP-Complete NP-Hard If you can show that a problem is equivalent can be reduced to a known NP-Complete problem you may as well not try to find an efficient solution for it unless youre convinced youre a genius If such a polynomial solution exists P NP It is not known whether P NP or P NP.
Source: hu.pinterest.com
Suppose we want to make am exam schedule for a university. Graph coloring problem is a NP Complete problem. This result is already known 18 but our proof is novel as it does not rely on the PCP theorem while the one in 18 does. Step 2 Choose the first vertex and color it with the first color. Garey and Johnson 10 proved that it is NP-hard to approximate the chromatic number within a factor of 2 for any 0The best known algorithm for general graphs appears in 13 and colors a graph using a number of.
Source: slidetodoc.com
This problem can be described as an np hard problem it means it cannot be solved in polynomial time algorithm. The graph coloring problem has huge number of applications. Garey and Johnson 10 proved that it is NP-hard to approximate the chromatic number within a factor of 2 for any 0The best known algorithm for general graphs appears in 13 and colors a graph using a number of. Graph coloring is one such heuristic algorithm that can deal timetable scheduling satisfying changing requirements evolving subject demands and. The reduction maps a graph ji into a new graph such that k 3-COLOR if and only if i 4-COLOR.
Source: geeksforgeeks.org
Check out the course here. 1 Making Schedule or Time Table. Step 1 Arrange the vertices of the graph in some order. Method to Color a Graph. The definition of coloring implies that GK is in K-COLORING iff Gk0 is in MIN-MONOCHROMATIC.
Source: pinterest.com
The graph coloring problem has huge number of applications. We show that obtaining the lexicographically rst four coloring of a planar graph is NPhard. So f is a polytime many-one reduction from an NP-hard problem K-COLORING to MIN-MONOCHROMATIC so we conclude that the latter is NP-hard. Step 2 Choose the first vertex and color it with the first color. This type of NP-Hard problem can be efficiently solved using graph coloring when compared to general graphs.
Source: slideserve.com
Corresponding optimization problem is NP Hard. A graph G is k-degenerate if each of its subgraphs has a vertex of degree at most k. This problem can be described as an np hard problem it means it cannot be solved in polynomial time algorithm. NP-Complete NP-Hard If you can show that a problem is equivalent can be reduced to a known NP-Complete problem you may as well not try to find an efficient solution for it unless youre convinced youre a genius If such a polynomial solution exists P NP It is not known whether P NP or P NP. This highlights a qualitative difference between the known hardness result for coloring 3-colorable graphs and the factor nε hardness for approximating the chromatic.
Source: penzba.co.uk
Suppose we want to make am exam schedule for a university. NP-Complete NP-Hard If you can show that a problem is equivalent can be reduced to a known NP-Complete problem you may as well not try to find an efficient solution for it unless youre convinced youre a genius If such a polynomial solution exists P NP It is not known whether P NP or P NP. A graph G is k-degenerate if each of its subgraphs has a vertex of degree at most k. Of colors is NP-hard 16 so the focus shifts to efficiently coloring a graph with an approximately optimum number of colors. This video is part of an online course Intro to Algorithms.
Source: quora.com
Given a graph G can you color the nodes with k colors such that the endpoints of every edge are colored di erently. The definition of coloring implies that GK is in K-COLORING iff Gk0 is in MIN-MONOCHROMATIC. This shows that planar graph four-coloring is not self-reducible assuming P6 NP. Since it is also in NP it is NP-complete. The degeneracy of G denoted δG is the smallest k such that G is k-degenerate.
Source: geeksforgeeks.org
The steps required to color a graph G with n number of vertices are as follows. We give a polynomial-time reduction from 3-COLOR to 4-COLOR. The problem to find chromatic number of a given graph is NP Complete. This shows that planar graph four-coloring is not self-reducible assuming P6 NP. NP-Complete NP-Hard If you can show that a problem is equivalent can be reduced to a known NP-Complete problem you may as well not try to find an efficient solution for it unless youre convinced youre a genius If such a polynomial solution exists P NP It is not known whether P NP or P NP.
Source: slidetodoc.com
Since it is also in NP it is NP-complete. We give a polynomial-time reduction from 3-COLOR to 4-COLOR. Is vertex coloring of a hypergraph with no uniformity restriction NP-hard. We have list different subjects and students enrolled in every subject. The steps required to color a graph G with n number of vertices are as follows.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your favorite social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring np hard by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
