Your Graph coloring np complete proof images are available. Graph coloring np complete proof are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring np complete proof files here. Get all free photos.
If you’re searching for graph coloring np complete proof images information linked to the graph coloring np complete proof keyword, you have come to the right site. Our site always gives you suggestions for seeing the highest quality video and image content, please kindly surf and find more informative video articles and graphics that fit your interests.
Graph Coloring Np Complete Proof. 54 3 Non-deterministic computation. Every node has one of two values. It is NP-complete to decide if a given graph admits a k-coloring for a given k except for the cases k 012. 3 Show that Y P X.
4 Color To 3 Color Polynomial Reduction Computer Science Stack Exchange From cs.stackexchange.com
One unfortunate restriction of polynomial time reductions is that we have to convert an instance of one problem into a singleinstance. The language -COLOR is defined to be the set of undirected graphs whose vertices can be colored with at most f distinct colors in such a way that no two adjacent vertices are colored the same color. Given a graph G VEwhere V 2n is an even number we can see that we have a bisection of size K or more if and only if the complement of G has a bisection of size n2 K. Given a graph G V E and a set of colors k V. Then we can check all of the edges in On which is absolutely a polynomial time complexity. If you had an algorithm to solve 4-coloring you could use it to test if a graph G is 3-colorable by adding a vertex adjacent to all others and testing if the new graph G is 4-colorable.
Given a graph G V E and a set of colors k V.
Prove NP Hardness. 2 Look at some problems that are known to be NP-complete there are thousands and choose one Y that seems similar to your problem in some way. Two adjacent vertices are in conflict if they have the same color. The reduction will be more or less difficult. Since 3-colorability is NP-complete all NP problems can be reduced to 3-coloring and then we can use this strategy to reduce them all to 4-coloring. N via colors for some nodes in Gφ.
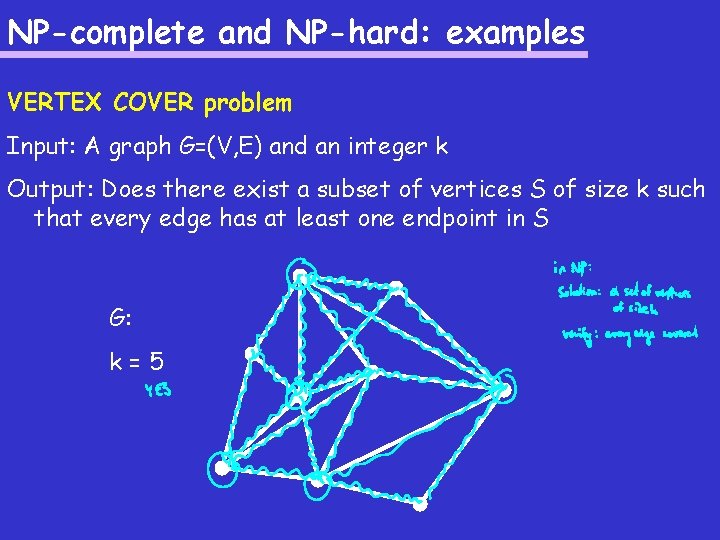Source: slidetodoc.com
Interpret this as a truth assignment to v i For each clause C j abc create a small gadget graph. The reduction will be more or less difficult. The language -COLOR is defined to be the set of undirected graphs whose vertices can be colored with at most f distinct colors in such a way that no two adjacent vertices are colored the same color. 54 3 Non-deterministic computation. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict.
Source: geeksforgeeks.org
2 Look at some problems that are known to be NP-complete there are thousands and choose one Y that seems similar to your problem in some way. Given a graph GVE return 1 if and only if there is a proper colouring of Gusing at most 3 colours. Every node has one of two values. As discussed in the previous post graph coloring is widely used. This has been added to last lectures notes.
Source: quora.com
Prove that 4-COLOR is NP-complete. Every variable has one of two values. Thus 3-Coloring is in NP. If we represent the graph using Adjacency Matrix A1n 1n where Aij1 if ij is an edge. Prove that 4-COLOR is NP-complete.
Source: quora.com
On the other hand greedy colorings can be arbitrarily bad. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be. 34 Turing reductions andNP-hardness. If you had an algorithm to solve 4-coloring you could use it to test if a graph G is 3-colorable by adding a vertex adjacent to all others and testing if the new graph G is 4-colorable. V G 1 2 k such that for each S V G 2 S 3 there exist u v S with f u f v at least the size of the subgraph induced by S.
Source: cs.stackexchange.com
The 3-coloring problem remains NP-complete even on 4-regular planar graphs. Graph coloring is computationally hard. In class we learned that 2-COLOR P and 3-COLOR is NP-complete. Planar graphs are 4-colorable k-coloring is NP-complete for k geq 3. Given a graph G V E and a set of colors k V.
Source: youtube.com
Prove NP Hardness. The reduction will be more or less difficult. On the other hand greedy colorings can be arbitrarily bad. To show the problem is in NP our veri er takes a graph GVE and a colouring c and checks in On2 time whether cis a proper coloring by checking if the end points of every edge e2 Ehave di erent colours. This is the biggest piece of a pie and where the familiarity with NP Complete problems pays.
Source: slideplayer.com
Given a graph G VEwhere V 2n is an even number we can see that we have a bisection of size K or more if and only if the complement of G has a bisection of size n2 K. Two adjacent vertices are in conflict if they have the same color. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict. Reduce an arbitrary instance of an NP complete problem to an instance of your problem. V G 1 2 k such that for each S V G 2 S 3 there exist u v S with f u f v at least the size of the subgraph induced by S.
Source: geeksforgeeks.org
To prove NP-completeness by Theorem 1 it suffices to show that every instance of the 3-colorability problem consisting of a graph G with maximum degree four can be polynomially reduced to an instance of the 3-colorability problem consisting of a triangle-flee graph G with maximum degree four in such a way that G is 3-colorable if and only if G is. Interpret this as a truth assignment to v i For each clause C j abc create a small gadget graph. Given a graph G V E and a set of colors k V. Do this by showing there is an certi cate that can be e ciently checked. Reduce an arbitrary instance of an NP complete problem to an instance of your problem.
Source: researchgate.net
Do this by showing there is an certi cate that can be e ciently checked. The 3-coloring problem remains NP-complete even on 4-regular planar graphs. Then we can check all of the edges in On which is absolutely a polynomial time complexity. Freceives colour 0 can be completed to give a proper 3-colouring of this graph with the colours 0 1 and red. This has been added to last lectures notes.
Source: geeksforgeeks.org
Though if you can prove that it is youve just won 1000000. If we represent the graph using Adjacency Matrix A1n 1n where Aij1 if ij is an edge. Do this by showing there is an certi cate that can be e ciently checked. 1 Must show that X 2NP. To show the problem is in NP our veri er takes a graph GVE and a colouring c and checks in On2 time whether cis a proper coloring by checking if the end points of every edge e2 Ehave di erent colours.
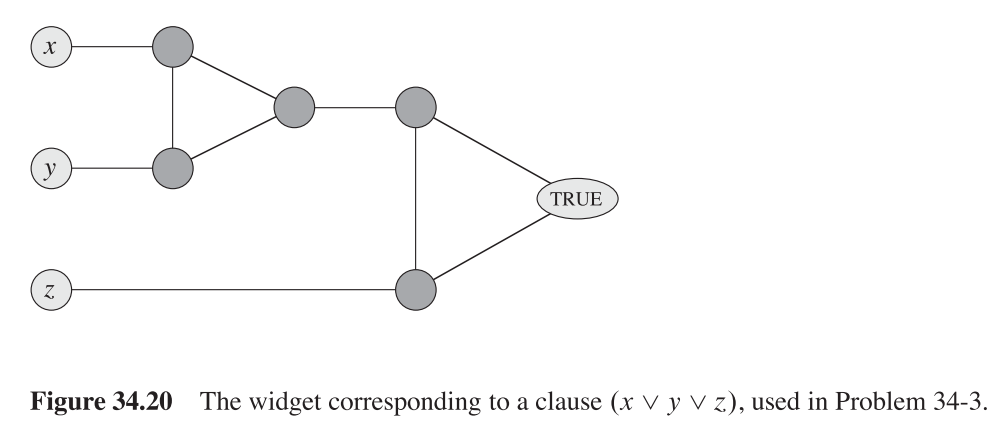Source: chegg.com
Though if you can prove that it is youve just won 1000000. Do this by showing there is an certi cate that can be e ciently checked. V G 1 2 k such that for each S V G 2 S 3 there exist u v S with f u f v at least the size of the subgraph induced by S. Graph coloring is computationally hard. 4-COLOR is in NP.
Source: slideplayer.com
Thus 3-Coloring is in NP. Then we can check all of the edges in On which is absolutely a polynomial time complexity. We prove that it is NP-complete to determine whether a planar graph has a local 5-coloring even restricted to the maximum degree Δ 7 or 8. Though if you can prove that it is youve just won 1000000. 54 3 Non-deterministic computation.
Source: youtube.com
We introduced graph coloring and applications in previous post. Given a graph G VEwhere V 2n is an even number we can see that we have a bisection of size K or more if and only if the complement of G has a bisection of size n2 K. 34 Turing reductions andNP-hardness. In class we learned that 2-COLOR P and 3-COLOR is NP-complete. Two adjacent vertices are in conflict if they have the same color.
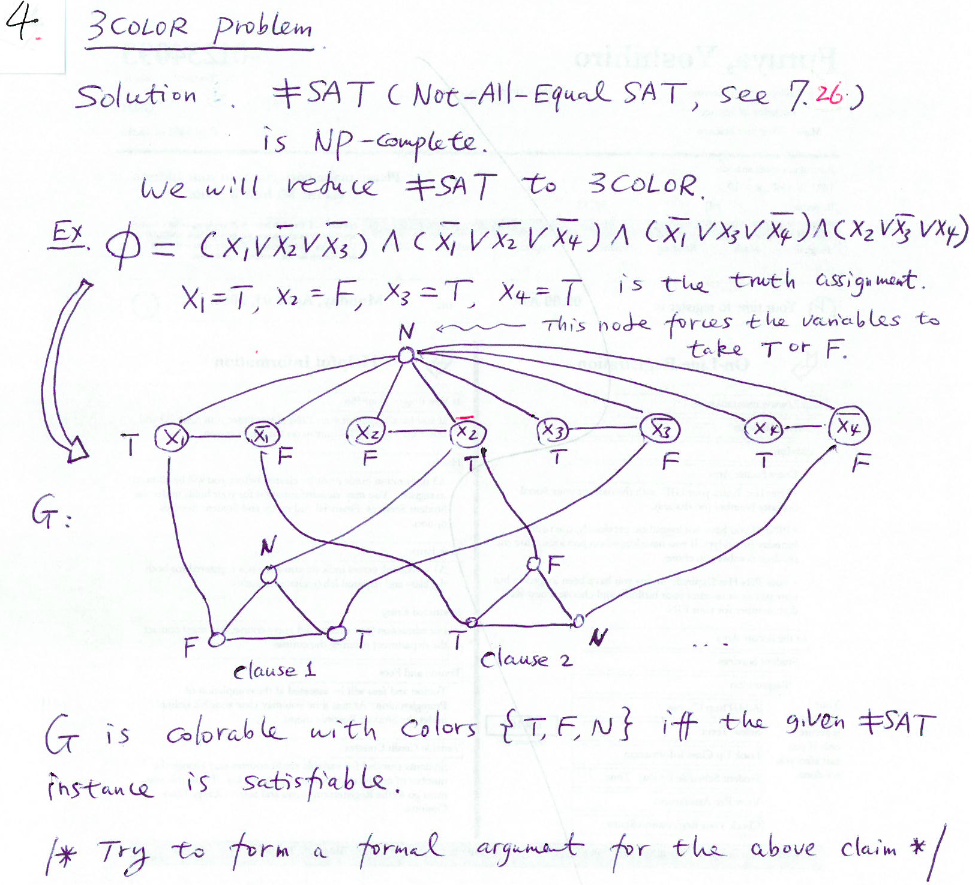Source: chegg.com
It would seem that 2COLOR whether a graph has a 2-coloring would be a better fit. Graph coloring is computationally hard. 3 Show that Y P X. Given a graph G V E and a set of colors k V. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict.
Source: mathoverflow.net
It says The quality of the resulting coloring depends on the chosen ordering. In class we learned that 2-COLOR P and 3-COLOR is NP-complete. Verticesxyorzreceives colour 1 the others receive colour 0 and vertex. Every variable has one of two values. BISECTION WIDTH is NP-complete.
Source: youtube.com
It is NP-complete to decide if a given graph admits a k-coloring for a given k except for the cases k 012. Proving NP-completeness of a graph coloring problem. We prove that it is NP-complete to determine whether a planar graph has a local 5-coloring even restricted to the maximum degree Δ 7 or 8. 54 3 Non-deterministic computation. If you had an algorithm to solve 4-coloring you could use it to test if a graph G is 3-colorable by adding a vertex adjacent to all others and testing if the new graph G is 4-colorable.
Source: semanticscholar.org
Given a graph G VEwhere V 2n is an even number we can see that we have a bisection of size K or more if and only if the complement of G has a bisection of size n2 K. The 3-coloring problem remains NP-complete even on 4-regular planar graphs. Proving NP-completeness of a graph coloring problem. It says The quality of the resulting coloring depends on the chosen ordering. General Strategy for Proving Something is NP-complete.
Source: researchgate.net
Verticesxyorzreceives colour 1 the others receive colour 0 and vertex. Do this by showing there is an certi cate that can be e ciently checked. Since 3-colorability is NP-complete all NP problems can be reduced to 3-coloring and then we can use this strategy to reduce them all to 4-coloring. 54 3 Non-deterministic computation. Every node has one of two values.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site convienient, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring np complete proof by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
