Your Graph coloring non planar images are ready in this website. Graph coloring non planar are a topic that is being searched for and liked by netizens today. You can Download the Graph coloring non planar files here. Find and Download all royalty-free images.
If you’re looking for graph coloring non planar pictures information connected with to the graph coloring non planar keyword, you have pay a visit to the right blog. Our site always gives you hints for downloading the highest quality video and image content, please kindly hunt and locate more enlightening video content and graphics that fit your interests.
Graph Coloring Non Planar. K 4 is a planar graph 3. De ne V0 Vfui j vi 2 Vg. Solution Number of vertices and edges in is 5 and 10 respectively. A graph is bipartite if and only if it is 2-colorable but not every bipartite graph is planar K 3 3 comes to mind.
Graph Coloring Wikiwand From wikiwand.com
The chromatic number of non-planar graphs can be more than four. The coloring theorems that will be discussed for planar graphs can actually be thought of as graphs on the sphere since a graph on the sphere can be made a graph on the plane by removing one point from the sphere. Actually colouring maps is a good motivation for the chromatic number problem but maybe not all that practical. Graph Coloring Algorithms Previous Work For any planar graph 4 colors. The graph can be pretty complex and is generally not planar and does not have any particular structure. Now for a connected planar graph 3v-e6.
Thus the graph is not planar.
In 1879 Alfred Kempe gave a proof that was widely known but was incorrect though it was. We can now solve the Problem of Three Houses and Three Utilities. A graph is 1-planar if it can be drawn on the plane. The relationship between basis cycles and a rim in a non-planar cubic graph and a ring sum of colored 2-factors is explicitly shown in the article. Hence G is non-planar. For example n for K_n.
Source: researchgate.net
But for non-planar more colors are neededknown as an NP-Hard problem. Note If is a connected planar graph with edges and vertices where then. A coloring of a simple graph is the assignment of a colour to each vertex of the graph so that no two adjacent vertices are assigned the same colour. We prove the problem to be NP-hard by exhibiting a simple reduction from the graph three colorability problem. Actually colouring maps is a good motivation for the chromatic number problem but maybe not all that practical.
Source: wikiwoh.blogspot.com
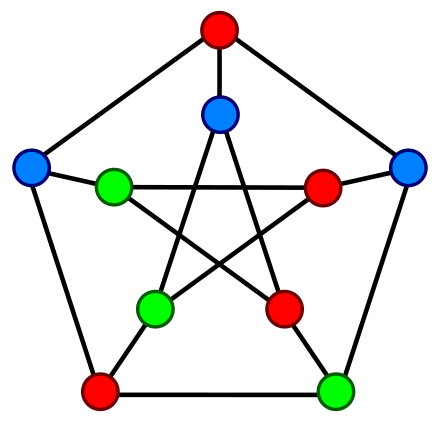
The complete graph K 5 contains 5 vertices and 10 edges. In this note we have given a non-trivial maximal planar graph in which a certain non-adjacent three vertices have the same color in any four colorings. Graph Coloring Algorithms Previous Work For any planar graph 4 colors. The Petersen Graph is 3-colorable and non-planar. Actually colouring maps is a good motivation for the chromatic number problem but maybe not all that practical.
Source: pinterest.com
The graph can be pretty complex and is generally not planar and does not have any particular structure. The coloring theorems that will be discussed for planar graphs can actually be thought of as graphs on the sphere since a graph on the sphere can be made a graph on the plane by removing one point from the sphere. Graph Coloring Algorithms Previous Work For any planar graph 4 colors. What is a Planar Graph. Hence for K 5 we have 3 x 5-105 which does not satisfy property 3 because it must be greater than or equal to 6.
Source: prideout.net
Hence G is non-planar. Then a graph can be coloured by assigning a different colour to each of its vertices. A graph is 1-planar if it can be drawn on the plane. Planar And Non Planar Graphs Javatpoint. A coloring of a simple graph is the assignment of a colour to each vertex of the graph so that no two adjacent vertices are assigned the same colour.
Source: researchgate.net
AbstractDrawings of non-planar graphs always result in edge crossings. Yifan Hu Lei Shi and Qingsong Liu. Obtaining the LF-4 coloring for a planar graph is NP-hard. For example n for K_n. We prove the problem to be NP-hard by exhibiting a simple reduction from the graph three colorability problem.
Source: pinterest.com
We know that p 6 and q 9. Planar and non planar graphs javatpoint. The smallest k for which such a coloring exists is called the neighbor sum distinguishing total choosability of G denoted by ch G. In this note we have given a non-trivial maximal planar graph in which a certain non-adjacent three vertices have the same color in any four colorings. Show that K 5 is non-planar.
Source: semanticscholar.org
Graph Coloring Algorithms Previous Work For any planar graph 4 colors. But for non-planar more colors are neededknown as an NP-Hard problem. When there are many edges crossing at small angles it is often difficult to follow these edges because of the multiple visual paths resulted from the crossings that slow down eye movements. Suppose we can represent K 33 as a plane graph. Obtaining the LF-4 coloring for a planar graph is NP-hard.
Source: pinterest.com
The Petersen Graph is 3-colorable and non-planar. Show that K 5 is non-planar. Dual of this maximal planar graph is an counterexample to the planar version of Geenwell and. When there are many edges crossing at small angles it is often difficult to follow these edges because of the multiple visual paths resulted from the crossings that slow down eye movements. The relationship between basis cycles and a rim in a non-planar cubic graph and a ring sum of colored 2-factors is explicitly shown in the article.
Source: wikiwoh.blogspot.com
The smallest k for which such a coloring exists is called the neighbor sum distinguishing total choosability of G denoted by ch G. The relationship between basis cycles and a rim in a non-planar cubic graph and a ring sum of colored 2-factors is explicitly shown in the article. A graph is non-planar if and only if it contains a subgraph homeomorphic to K 5 or K 33. The chromatic number of non-planar graphs can be more than four. So we need to understand something about r.
Source: wikiwand.com
In addition the relationship between the colored vertex rotation of a plane cubic graph and the closed Heawood paths is. Thus the graph is not planar. Planar And Non Planar Graphs Javatpoint. A graph is bipartite if and only if it is 2-colorable but not every bipartite graph is planar K 3 3 comes to mind. Show that K 5 is non-planar.
Source: researchgate.net
The smallest k for which such a coloring exists is called the neighbor sum distinguishing total choosability of G denoted by ch G. Theorem 5 The graph K 33 is not planar. The idea is to find a theorem that can limit the number of colors used to make the selection function of the voracious algorithm computationally simple. In addition the relationship between the colored vertex rotation of a plane cubic graph and the closed Heawood paths is. This problem was first posed in the nineteenth century and it was quickly conjectured that in all cases four colors suffice.
Source: researchgate.net
The article also addresses the issues of coloring non-planar cubic graphs. A coloring of a simple graph is the assignment of a colour to each vertex of the graph so that no two adjacent vertices are assigned the same colour. Show that K 5 is non-planar. The Petersen Graph is 3-colorable and non-planar. When there are many edges crossing at small angles it is often difficult to follow these edges because of the multiple visual paths resulted from the crossings that slow down eye movements.
Source: mdpi.com
A coloring of a simple graph is the assignment of a colour to each vertex of the graph so that no two adjacent vertices are assigned the same colour. In addition the relationship between the colored vertex rotation of a plane cubic graph and the closed Heawood paths is. The chromatic number of non-planar graphs can also be small. Hence G is non-planar. Dual of this maximal planar graph is an counterexample to the planar version of Geenwell and.
Source: slidetodoc.com
Properties of Non-Planar Graphs. Such a drawing is called a planar representation of the graph in the plane. Show that K 5 is non-planar. Planar And Non Planar Graphs Javatpoint. Hence for K 5 we have 3 x 5-105 which does not satisfy property 3 because it must be greater than or equal to 6.
Source: researchgate.net
Thus the graph is not planar. The smallest k for which such a coloring exists is called the neighbor sum distinguishing total choosability of G denoted by ch G. Thus the graph is not planar. Planar And Non Planar Graphs Javatpoint. Then a graph can be coloured by assigning a different colour to each of its vertices.
Source: piptools.net
Actually colouring maps is a good motivation for the chromatic number problem but maybe not all that practical. Yifan Hu Lei Shi and Qingsong Liu. K 4 is a planar graph 3. We prove the problem to be NP-hard by exhibiting a simple reduction from the graph three colorability problem. Planar and non planar graphs javatpoint.
Source: wikiwoh.blogspot.com
Dual of this maximal planar graph is an counterexample to the planar version of Geenwell and. Planar And Non Planar Graphs Javatpoint. This was finally proved in 1976 see figure 5103 with the aid of a computer. Then a graph can be coloured by assigning a different colour to each of its vertices. The chromatic number of non-planar graphs can also be small.
Source: pinterest.com
Yifan Hu Lei Shi and Qingsong Liu. Corollary 4 Any representation of a planar graph as a plane graph has the same number of regions. In addition the relationship between the colored vertex rotation of a plane cubic graph and the closed Heawood paths is. Note If is a connected planar graph with edges and vertices where then. This problem was first posed in the nineteenth century and it was quickly conjectured that in all cases four colors suffice.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring non planar by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
