Your Graph coloring lower bounds images are available in this site. Graph coloring lower bounds are a topic that is being searched for and liked by netizens today. You can Get the Graph coloring lower bounds files here. Get all royalty-free images.
If you’re looking for graph coloring lower bounds pictures information related to the graph coloring lower bounds topic, you have come to the ideal blog. Our website frequently provides you with suggestions for seeking the maximum quality video and picture content, please kindly hunt and locate more enlightening video articles and images that match your interests.
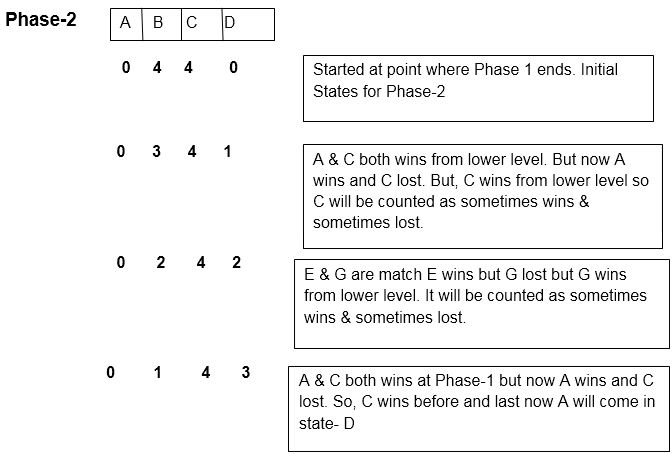
Graph Coloring Lower Bounds. The first one constructs bipartite graphs and forces any on-line coloring algorithm to use colors where is the number of vertices in the constructed graph. We introduce an iterative framework for computing lower bounds to graph coloring problems. The previous best lower bounds known were R log n for trees 14 lo and R logk n for k-colorable graphs where k is fixed 15. The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph.
Daa Lower Bound Theory Javatpoint From javatpoint.com
The features include presenting the input in blocks of log 2 n vertices recoloring any fraction of the vertices presorting vertices according to degree and disclosing the adversarys previous coloring. The first slighty-hard case is the triangular prism which is 3-colorable but for which some choices of minimum-degree vertex lead to a 4-coloring. The best method known for determining lower bounds on the vertex coloring number of a graph is the linear-programming column-generation technique where variables correspond to stable sets first. Ωllogn roundds needdded ffor O1O1coliloring a riing Linial92 General Graphs. To see that this number is actually indicative of the progress made notice that the. In this paper we prove a 2nlog2 n lower bound for deterministic on-line graph coloring which holds to within a constant factor for randomized algorithms.
Mathis Isaksen Accuracy of lower bounds We know that G G If G C 2n1.
It is all completely free—–Follow Youtube. Upper Bound of XG To obtain an upper bound for XG we. Graph coloring Lecture notes vol. Variations of the on-line modelsOn-line computing. The first one constructs bipartite graphs and forces any on-line coloring algorithm to use colors where is the number of vertices in the constructed graph. This algorithm is known as smallest-last coloring.
Source: pinterest.com
Since this graph contains the complete graph K 4 therefore XG 4. Mathis Isaksen Accuracy of lower bounds We know that G G If G C 2n1. We utilize relaxed decision diagrams to compactly represent an exponential set of color classes or independent sets some of which may contain edge conflicts. BikkiMahatoThe best part is. 1 did t I.
Source: ar.pinterest.com
Ωllogn roundds needdded ffor O1O1coliloring a riing Linial92 General Graphs. We introduce an iterative framework for computing lower bounds to graph coloring problems. Read Randomly coloring graphs with lower bounds on girth and maximum degree Random Structures and Algorithms on DeepDyve the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. To see that this number is actually indicative of the progress made notice that the. Basic Greedy Coloring Algorithm.
Source: pinterest.com
We present an implementation of the method that provides numerically safe results independent of the floating-point accuracy of linear-programming software. Following is the basic Greedy Algorithm to assign colors. This is best possible up to an additive constant. Variations of the on-line modelsOn-line computing. We propose two strategies for Presenter in on-line graph coloring games.
Source: javatpoint.com
The previous best lower bounds known were R log n for trees 14 lo and R logk n for k-colorable graphs where k is fixed 15. The best known method for determining lower bounds on the vertex coloring number of a graph is the linear-programming column-generation technique first employed by Mehrotra and Trick in 1996. Lower bounds for on-line graph coloring 167 progress is the number of distinct pairs of bin and color values assigned to the vertices or I Binoi COlO. 4 Accuracy of lower bounds probabilistic method and of some constructions Lecturer. 1 did t I.
Source: javatpoint.com
The previous best lower bounds known were R log n for trees 14 lo and R logk n for k-colorable graphs where k is fixed 15. Since this graph contains the complete graph K 4 therefore XG 4. Lower bounds for on-line graph colorings. Is there a graph with G 2 and G 4. Variations of the on-line modelsOn-line computing.
Source: pinterest.com
Variations of the on-line modelsOn-line computing. Lower bounds for on-line graph coloring 167 progress is the number of distinct pairs of bin and color values assigned to the vertices or I Binoi COlO. Graph coloring Lecture notes vol. Read Randomly coloring graphs with lower bounds on girth and maximum degree Random Structures and Algorithms on DeepDyve the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. It is all completely free—–Follow Youtube.
Source: variationtheory.com
Read Randomly coloring graphs with lower bounds on girth and maximum degree Random Structures and Algorithms on DeepDyve the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. Following is the basic Greedy Algorithm to assign colors. To see that this number is actually indicative of the progress made notice that the. It is all completely free—–Follow Youtube. 4 Accuracy of lower bounds probabilistic method and of some constructions Lecturer.
Source: pinterest.com
Color first vertex with first color. N 2 then G 2. Lower bounds for on-line graph colorings. The best method known for determining lower bounds on the vertex coloring number of a graph is the linear-programming column-generation technique where variables correspond to stable sets first. BikkiMahatoThe best part is.
Source: pinterest.com
Our measure of Lower bounds for on-line graph coloring 167 progress is the number of distinct pairs of bin and color values assigned to the vertices or iBinviColvi. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors. Ωllogn roundds needdded ffor O1O1coliloring a riing Linial92 General Graphs. This algorithm is known as smallest-last coloring. Safe Lower Bounds For Graph Coloring Stephan Held Edward C.
Source: pinterest.com
G 3 Q. Mathis Isaksen Accuracy of lower bounds We know that G G If G C 2n1. We also show that various means of relaxing the constraints of the on-line model do not reduce these lower bounds. Following is the basic Greedy Algorithm to assign colors. Basic Greedy Coloring Algorithm.
Source: in.pinterest.com
Following is the basic Greedy Algorithm to assign colors. The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph. 4 Accuracy of lower bounds probabilistic method and of some constructions Lecturer. We also show that various means of relaxing the constraints of the on-line model do not reduce these lower bounds. Since this graph contains the complete graph K 4 therefore XG 4.
Source: slideplayer.com
We introduce an iterative framework for computing lower bounds to graph coloring problems. Is there a graph with G 2 and G 4. Lower Bound of XG To obtain a lower bound for XG we look for the largest complete subgraph in G. To see that this number is actually indicative of the progress made notice that the. Our measure of Lower bounds for on-line graph coloring 167 progress is the number of distinct pairs of bin and color values assigned to the vertices or iBinviColvi.
Source: math24.net
The best known method for determining lower bounds on the vertex coloring number of a graph is the linear-programming column-generation technique first employed by Mehrotra and Trick in 1996. Since this graph contains the complete graph K 4 therefore XG 4. Color first vertex with first color. This algorithm is known as smallest-last coloring. Is there a graph with G 2 and G 4.
Source: javatpoint.com
Sewell William Cook November 8 2010 Abstract Thebestknownmethodfordetermininglowerboundsonthevertexcoloringnum-ber of a graph. G 3 Q. Following is the basic Greedy Algorithm to assign colors. Δ1coloring in time OΔ2logn GoldbergPlotkinShannon 88 OΔ2coloring in time Ologn Linial 92 Δ1coloring in time OΔlog n Awerbuch et al. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors.
Source: slideplayer.com
To see that this number is actually indicative of the progress made notice that the. Sewell William Cook November 8 2010 Abstract Thebestknownmethodfordetermininglowerboundsonthevertexcoloringnum-ber of a graph. We utilize relaxed decision diagrams to compactly represent an exponential set of color classes or independent sets some of which may contain edge conflicts. The previous best lower bounds known were R log n for trees 14 lo and R logk n for k-colorable graphs where k is fixed 15. Basic Greedy Coloring Algorithm.
Source: javatpoint.com
We also show that various means of relaxing the constraints of the on-line model do not reduce these lower bounds. 1 did t I. This algorithm is known as smallest-last coloring. Basic Greedy Coloring Algorithm. Lower bounds for on-line graph coloring 167 progress is the number of distinct pairs of bin and color values assigned to the vertices or I Binoi COlO.
Source: pinterest.com
This is best possible up to an additive constant. Read Randomly coloring graphs with lower bounds on girth and maximum degree Random Structures and Algorithms on DeepDyve the largest online rental service for scholarly research with thousands of academic publications available at your fingertips. 1 did t I. To see that this number is actually indicative of the progress made notice that the number of bins is at least the number of bincolor pairs divided by the maximum number of pairs with the same bin number. We utilize relaxed decision diagrams to compactly represent an exponential set of color classes or independent sets some of which may contain edge conflicts.
Source: pinterest.com
1 did t I. Upper Bound of XG To obtain an upper bound for XG we. The best method known for determining lower bounds on the vertex coloring number of a graph is the linear-programming column-generation technique where variables correspond to stable sets first. Sewell William Cook November 8 2010 Abstract Thebestknownmethodfordetermininglowerboundsonthevertexcoloringnum-ber of a graph. To see that this number is actually indicative of the progress made notice that the number of bins is at least the number of bincolor pairs divided by the maximum number of pairs with the same bin number.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring lower bounds by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
