Your Graph coloring in register allocation images are ready. Graph coloring in register allocation are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring in register allocation files here. Get all free images.
If you’re searching for graph coloring in register allocation pictures information linked to the graph coloring in register allocation keyword, you have visit the ideal site. Our site frequently provides you with suggestions for refferencing the maximum quality video and image content, please kindly hunt and find more enlightening video content and graphics that fit your interests.
Graph Coloring In Register Allocation. This and cu-riosity - lead to the implementation of a more traditional graph coloring register allocator for GCC. 2 Graph Coloring Register Alloca-tors This section describes graph coloring register. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively. In the context of space allocation each unit of space register is a color and each variable is a node.
Register Allocations In Code Generation Geeksforgeeks From geeksforgeeks.org
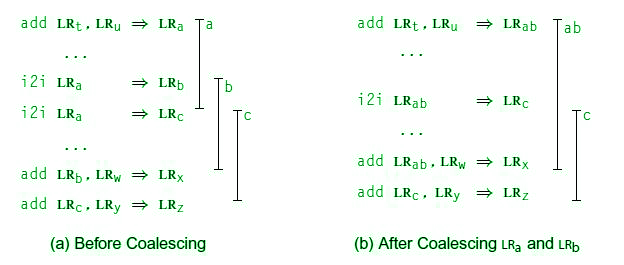
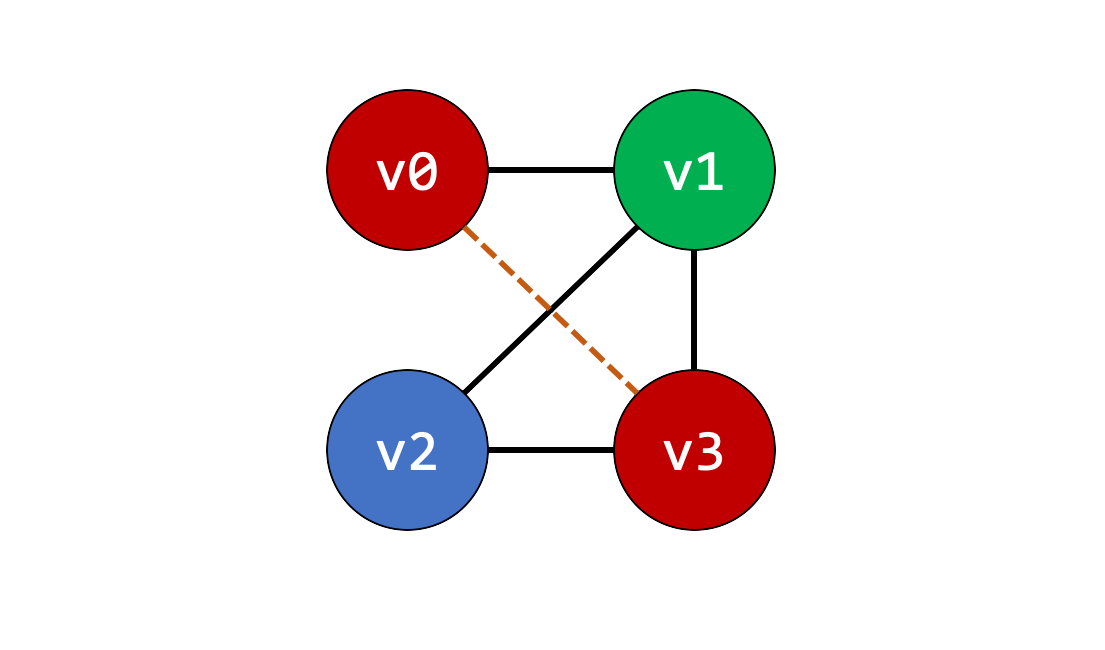
A k-coloring of the graph is. Registers are the fastest locations in the memory hierarchy. Despite the existence of reasonably good allocation algorithms the need for improved algorithms persists. 429 absolute demand for registers. Assigning color to the nodes such that no two adjacent nodes have same color. If two program variables are live at the same time4 then they must not be assigned to the same registerthis situation is indicated by placing anedge in the interference graph.
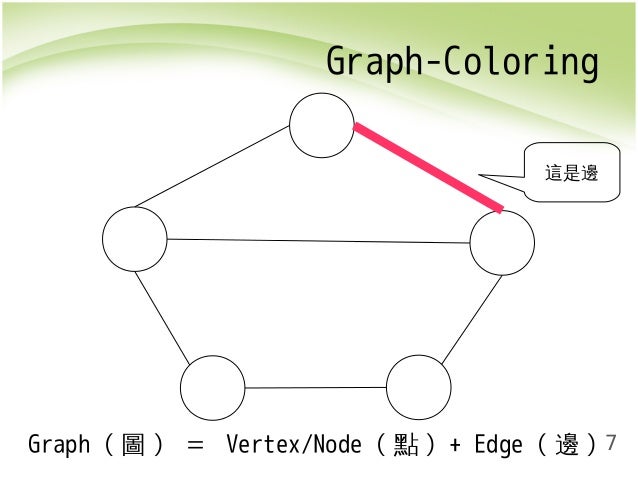
This graph is known as an interference graph.
Popular techniques for performing register allocation are based on a graph. The algorithm was designed to allocate space registers to variables in a program but is written so it can be generalized to other contexts as well. However this problem can be reduced to graph coloring to achieve allocation and. If two program variables are live at the same time4 then they must not be assigned to the same registerthis situation is indicated by placing anedge in the interference graph. In this approach nodes in the graph represent variables and edges represent live range conflicts. Keywordschromatic number interference graph graph coloring register allocation.
Source: slidetodoc.com
The variables of the program are treated as vertices in an interference graph. In this paper we examine the importance of the quality of the coloring algorithm and various extensions of the basic. Despite the existence of reasonably good allocation algorithms the need for improved algorithms persists. Edges represent the connection between two live ranges. It comes under the most constrained resources of the target processor.
Source: slideshare.net
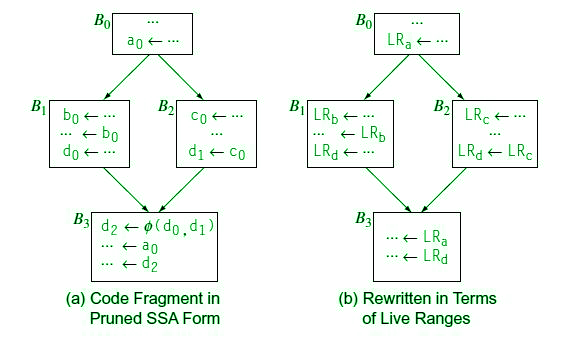
Our generalization permits simultaneous allocation of mul-tiple register classes even when registers alias while maintaining the efficiency and general structure of the original graph-coloring formulation. 429 absolute demand for registers. Register Allocation via Graph Coloring The basic idea behind register allocation via graph coloring is to reduce register spillage by globally assigning variables to registers across an entire program module via the five basic steps below. Assigning color to the nodes such that no two adjacent nodes have same color. This graph is known as an interference graph.
Source:
A complete treatment of the graph colouring approach to register allocation involves a pipeline of analysis and code transformations that goes well beyond what can routinely be achieved in a three-hour test. In the context of space allocation each unit of space register is a color and each variable is a node. Registers are the fastest locations in the memory hierarchy. This naturally increases the demand for registers. Assigning color to the nodes such that no two adjacent nodes have same color.
Source: geeksforgeeks.org
Both algorithms construct and color an interference graph that rep-resents correctnessconstraints. In this paper we examine the importance of the quality of the coloring algorithm and various extensions of the basic. Edges represent the connection between two live ranges. Koblenz hierarchical allocator7 that map the register allocation problem to a graph coloring problem. This and cu-riosity - lead to the implementation of a more traditional graph coloring register allocator for GCC.
Source: slideshare.net
In this paper we examine the importance of the quality of the coloring algorithm and various extensions of the basic. If the machine issues two instructions in a single cycle it must have two sets of operands ready and in place at the start of the cycle. The algorithm was designed to allocate space registers to variables in a program but is written so it can be generalized to other contexts as well. The first opti- mistic coloring uses a stronger heuristic to find a k -coloring for the interference graph. If two program variables are live at the same time4 then they must not be assigned to the same registerthis situation is indicated by placing anedge in the interference graph.
Source: pinterest.com
Many current com- pilers use graph coloring to do register allocation. This paper generalizes the graph-coloring approach to register allocation in a way that eliminates the need for the kinds of workarounds currently employed formodern commercial architec-tures. Keywordschromatic number interference graph graph coloring register allocation. However this problem can be reduced to graph coloring to achieve allocation and. The colors used to.
Source: slideshare.net
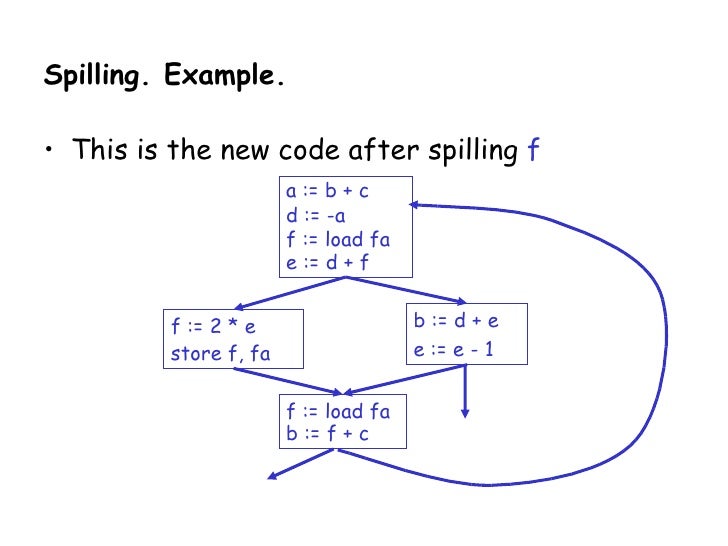
W e describ e tw o improv ements to Chaitin-style graph coloring register allocators. In the context of space allocation each unit of space register is a color and each variable is a node. W e describ e tw o improv ements to Chaitin-style graph coloring register allocators. The register allocator itself and that it is done on a per instruction basis leads to non-optimal spill code in some situations. Register allocation is an NP-complete problem.
Source: chrisseaton.com
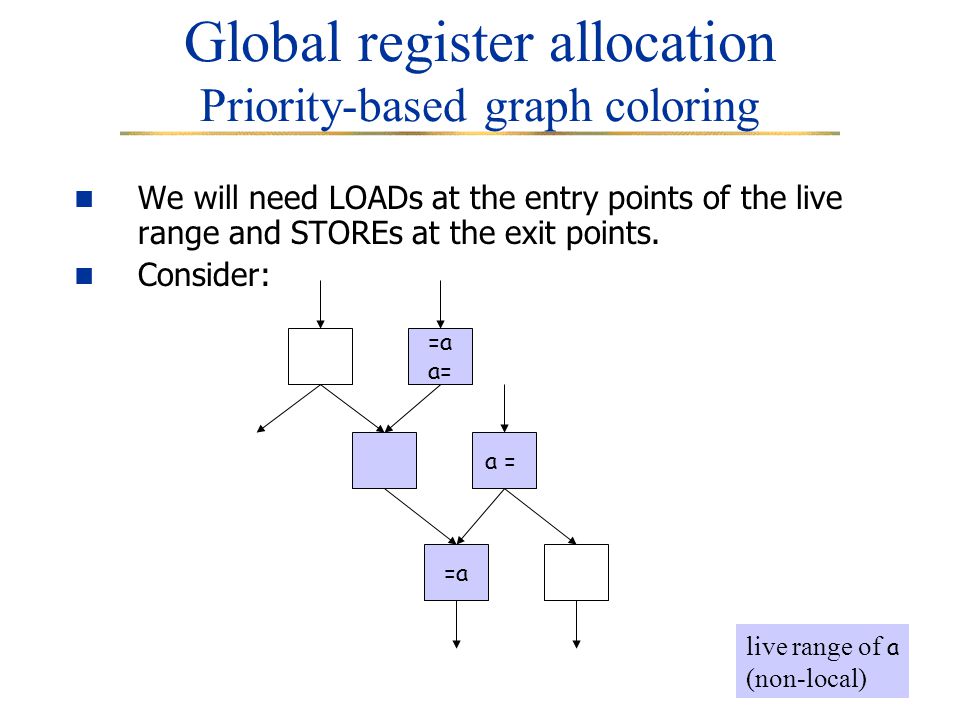
The algorithm was designed to allocate space registers to variables in a program but is written so it can be generalized to other contexts as well. The process consists of creating a control flow graph computing alive variables at each point constructing interference graph and coloring graph. Registers are the fastest locations in the memory hierarchy. For example global register allocation procedure. The register allocator itself and that it is done on a per instruction basis leads to non-optimal spill code in some situations.
Source: slideshare.net
Despite the existence of reasonably good allocation algorithms the need for improved algorithms persists. The register allocator itself and that it is done on a per instruction basis leads to non-optimal spill code in some situations. This graph is known as an interference graph. In the context of space allocation each unit of space register is a color and each variable is a node. The variables of the program are treated as vertices in an interference graph.
Source:
For example global register allocation procedure. Keywordschromatic number interference graph graph coloring register allocation. The variables of the program are treated as vertices in an interference graph. Assigning color to the nodes such that no two adjacent nodes have same color. This and cu-riosity - lead to the implementation of a more traditional graph coloring register allocator for GCC.
Source: geeksforgeeks.org
Nodes represent live range of the variable. 2 Graph Coloring Register Alloca-tors This section describes graph coloring register. Despite the existence of reasonably good allocation algorithms the need for improved algorithms persists. In this paper we examine the importance of the quality of the coloring algorithm and various extensions of the basic. Graph coloring is a powerful tool for compilers to optimize the code so that register allocation can be done effectively.
Source: chrisseaton.com
However this problem can be reduced to graph coloring to achieve allocation and. This and cu-riosity - lead to the implementation of a more traditional graph coloring register allocator for GCC. But unfortunately this resource is limited. As can be expected optimal coloringof the interference graph is also NP-complete and the allocators resort to heuristics to color the graph. If two program variables are live at the same time4 then they must not be assigned to the same registerthis situation is indicated by placing anedge in the interference graph.
Source: pinterest.com
The process consists of creating a control flow graph computing alive variables at each point constructing interference graph and coloring graph. Based on Graph Theory graph coloring assigns colors to each node such that no two adjacent nodes share the same color. But unfortunately this resource is limited. Register Allocations in Code Generation. Both algorithms construct and color an interference graph that rep-resents correctnessconstraints.
Source: geeksforgeeks.org
A complete treatment of the graph colouring approach to register allocation involves a pipeline of analysis and code transformations that goes well beyond what can routinely be achieved in a three-hour test. However this problem can be reduced to graph coloring to achieve allocation and. Assign each object intermediate result name variable or constant to a distinct symbolic register. The process consists of creating a control flow graph computing alive variables at each point constructing interference graph and coloring graph. Register allocation via graph coloring was invented by Chaitin et al.
Source: pinterest.com
However this problem can be reduced to graph coloring to achieve allocation and. The predominant approach to analyzing variable lifetimes and allocating registers is through graph coloring. Koblenz hierarchical allocator7 that map the register allocation problem to a graph coloring problem. It comes under the most constrained resources of the target processor. Graph coloring is the de facto standard technique for register allocation within a compiler.
Source: pinterest.com
However this problem can be reduced to graph coloring to achieve allocation and. However this problem can be reduced to graph coloring to achieve allocation and. It comes under the most constrained resources of the target processor. If two program variables are live at the same time4 then they must not be assigned to the same registerthis situation is indicated by placing anedge in the interference graph. Keywordschromatic number interference graph graph coloring register allocation.
Source: geeksforgeeks.org
Assign each object intermediate result name variable or constant to a distinct symbolic register. Improvements to Graph Coloring Register Allocation. Assign each object intermediate result name variable or constant to a distinct symbolic register. This paper generalizes the graph-coloring approach to register allocation in a way that eliminates the need for the kinds of workarounds currently employed formodern commercial architec-tures. However this problem can be reduced to graph coloring to achieve allocation and.
Source: slideplayer.com
Register allocation via graph coloring was invented by Chaitin et al. Koblenz hierarchical allocator7 that map the register allocation problem to a graph coloring problem. Both algorithms construct and color an interference graph that rep-resents correctnessconstraints. For example global register allocation procedure. But unfortunately this resource is limited.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site adventageous, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring in register allocation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
