Your Graph coloring greedy algorithm time complexity images are ready. Graph coloring greedy algorithm time complexity are a topic that is being searched for and liked by netizens now. You can Download the Graph coloring greedy algorithm time complexity files here. Download all royalty-free vectors.
If you’re searching for graph coloring greedy algorithm time complexity pictures information connected with to the graph coloring greedy algorithm time complexity topic, you have come to the ideal site. Our website frequently provides you with suggestions for seeing the maximum quality video and picture content, please kindly hunt and locate more enlightening video articles and graphics that fit your interests.
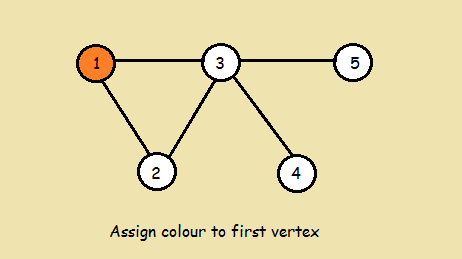
Graph Coloring Greedy Algorithm Time Complexity. Color first vertex with first color. So the time complexity is OmV. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Finding a polynomial-time greedy algorithm for providing solutions to graph coloring.
Welsh Powell Graph Colouring Algorithm Geeksforgeeks From geeksforgeeks.org
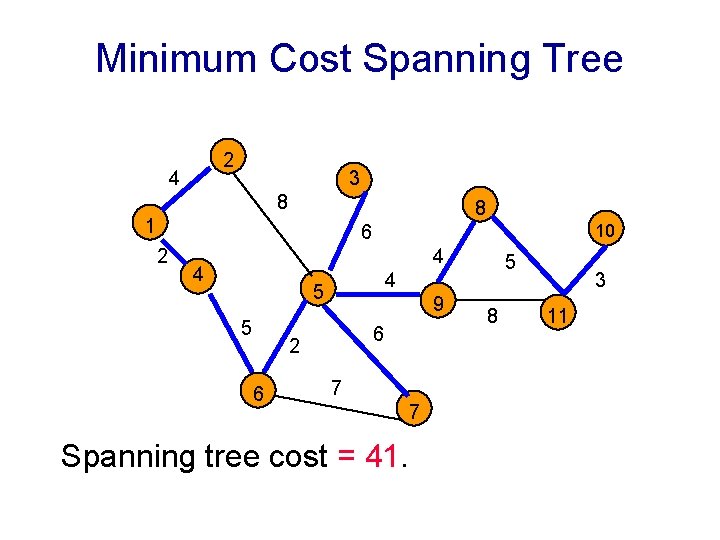
Algorithm for graph coloring problem colors. It is to be noted that the upperbound time complexity remains the same but the average time taken will be less due to the refined approach. The time complexity for Kruskals algorithm is OElogE or OElogV. OV for storing the output array in OV space. A basic solution to this would be a backtracking algorithm. So the time complexity is OmV.
1 online algorithms for edge coloring by Feder Motwani Panigrahy.
The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph. Sorting of all the edges has the complexity OElogE. Algorithm for graph coloring problem colors. Since backtracking is also a kind of brute force approach there would be total Om V possible color combinations. Here E and V represent the number of edges and vertices in the given graph respectively. In this paper we give a polynomial time algorithm to find the total coloring of a graph 𝐺 and we discuss about the time complexity.
Source: pinterest.com
Sorting of all the edges has the complexity OElogE. The maximum worst number of colors that can be obtained by the greedy algorithm by using a vertex ordering chosen to maximize this number is called the Grundy number of a graph. Here E and V represent the number of edges and vertices in the given graph respectively. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. We observe that the popular greedy heuristic works poorly on k-colorable graphs.
Source: geeksforgeeks.org
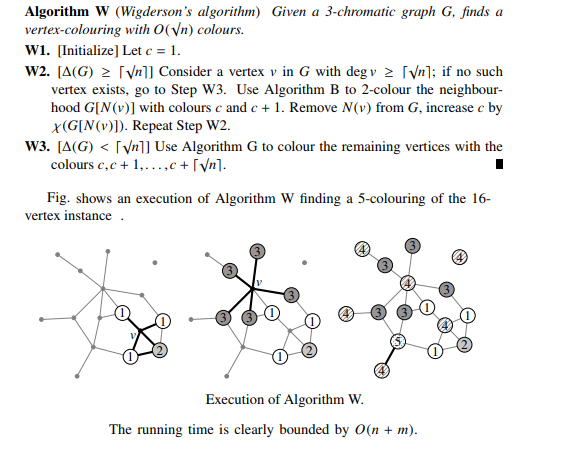
16 the time complexity is the number of rounds until the algorithm terminates. 1 online algorithms for edge coloring by Feder Motwani Panigrahy. Theorem 18 Analysis of Algorithm 3. The above facts suggest the greedy algorithm used which at most will use n colors but often less than n colors unless every vertex is connected to each other although not optimal in general. Time and space analayis Assume the graph is given as an adjacency list in some form and that it takes constant time to get the outdegree of a vertex.
Source: slidetodoc.com
Time Complexity of Kruskals algorithm. In this paper we give a polynomial time algorithm to find the total coloring of a graph 𝐺 and we discuss about the time complexity. There is a total OmV combination of colors. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
Source: iq.opengenus.org
2 Total Coloring Algorithm Aim. The maximum worst number of colors that can be obtained by the greedy algorithm by using a vertex ordering chosen to maximize this number is called the Grundy number of a graph. Graph coloring is a special case of graph labeling. Finding a polynomial-time greedy algorithm for providing solutions to graph coloring. From my understanding for problems like this greedy might not always give a correct solution since a graph may contain cycles and you might not be aware of certain edges to nodes until you reduce your space to a few nodes and youre left with incompatible colors.
Source: iq.opengenus.org
The above facts suggest the greedy algorithm used which at most will use n colors but often less than n colors unless every vertex is connected to each other although not optimal in general. To store the output array OV space is required. The number of colors used in the graph depends on the order of. The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph. Here E and V represent the number of edges and vertices in the given graph respectively.
Source: iq.opengenus.org
Before assigning a color check for safety by. Greedy coloring doesnt always use the minimum number of colors possible to color a graph. The time complexity for Kruskals algorithm is OElogE or OElogV. OV for storing the output array in OV space. The current state-of-the-art randomized algorithms are faster for.
Source: interviewbit.com
Before assigning a color check for safety by. To store the output array OV space is required. Algorithm for graph coloring problem colors. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors. Time Complexity of Kruskals algorithm.
Source: in.pinterest.com
It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Space complexity of the algorithm and as the time. Greedy coloring doesnt always use the minimum number of colors possible to color a graph. Here E and V represent the number of edges and vertices in the given graph respectively. Sorting of all the edges has the complexity OElogE.
Source: pinterest.com
Algorithm to color the graph is given to the right. The time complexity of a distributed algorithm then is the maximum possible number of rounds needed until every node has completed its computation. Sorting of all the edges has the complexity OElogE. 2 Total Coloring Algorithm Aim. The algorithm uses 1colors.
Source: iq.opengenus.org
After sorting we apply the find-union algorithm for each edge. Step 1- Find edge independent set. Algorithm to color the graph is given to the right. Space complexity of the algorithm and as the time. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors.
Source: geeksforgeeks.org
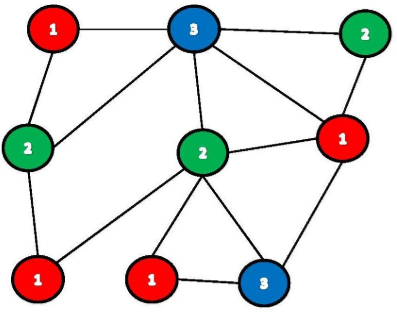
Following is the basic Greedy Algorithm to assign colors. Loop through each vertex and assign an available color based on available colors list not used on colors of adjacent vertices. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors. NThe graph ehas vertices and edges.
Source: geeksforgeeks.org
In this paper we give a polynomial time algorithm to find the total coloring of a graph 𝐺 and we discuss about the time complexity. Basic Greedy Coloring Algorithm. The idea is to assign colors one by one to different vertices starting from the vertex 0. Algorithm 3 is correct and has time complexity n. In the field of distributed algorithms graph coloring is closely related to the problem of symmetry breaking.
Source: slidetodoc.com
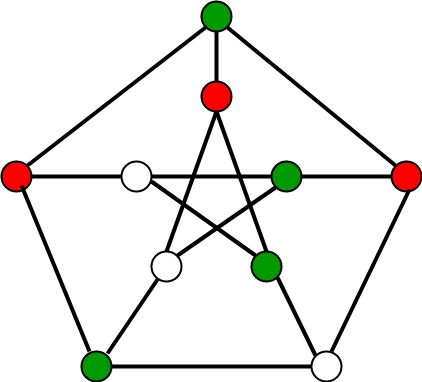
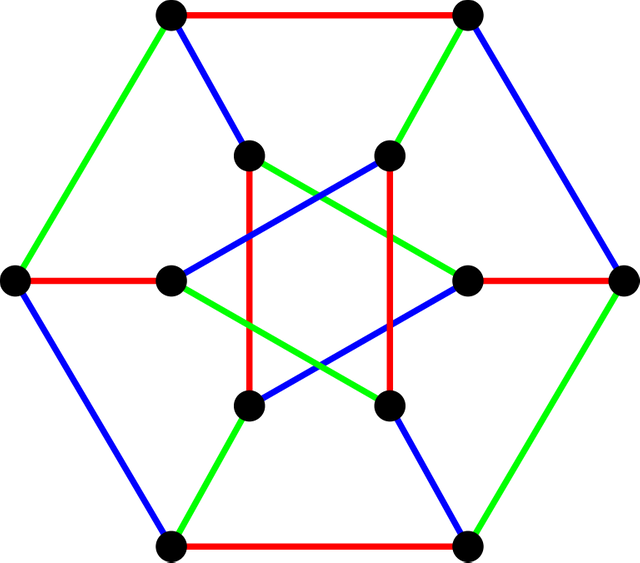
It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. For example the following crown graph a complete bipartite graph having n vertices can be 2colored refer left image but greedy coloring resulted in n2 colors refer right image. There is a total OmV combination of colors. The time complexity for Kruskals algorithm is OElogE or OElogV. For a graph of maximum degree x greedy coloring will use at most x1 color.
Source: in.pinterest.com
15 minutes Coding time. 2 Total Coloring Algorithm Aim. It is to be noted that the upperbound time complexity remains the same but the average time taken will be less due to the refined approach. Finding a polynomial-time greedy algorithm for providing solutions to graph coloring. Greedy coloring can be arbitrarily bad.
Source: steemit.com
There are total OmV combination of colors. Loop through each vertex and assign an available color based on available colors list not used on colors of adjacent vertices. NThe graph ehas vertices and edges. For a graph of maximum degree x greedy coloring will use at most x1 color. Greedy coloring can be arbitrarily bad.
Source: pinterest.com
The upperbound time complexity remains the same but the average time taken will be less. Greedy coloring doesnt always use the minimum number of colors possible to color a graph. Loop through each vertex and assign an available color based on available colors list not used on colors of adjacent vertices. In this paper we give a polynomial time algorithm to find the total coloring of a graph 𝐺 and we discuss about the time complexity. The above facts suggest the greedy algorithm used which at most will use n colors but often less than n colors unless every vertex is connected to each other although not optimal in general.
Source: researchgate.net
Greedy coloring can be arbitrarily bad. V 1s of colors between 1 and s to nodes such that adjacent nodes have different colors. Time and space analayis Assume the graph is given as an adjacency list in some form and that it takes constant time to get the outdegree of a vertex. 1 online algorithms for edge coloring by Feder Motwani Panigrahy. Color first vertex with first color.
Source: in.pinterest.com
Algorithm to color the graph is given to the right. There are total OmV combination of colors. Algorithm 3 is correct and has time complexity n. Basic Greedy Coloring Algorithm. Color first vertex with first color.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site serviceableness, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring greedy algorithm time complexity by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
