Your Graph coloring example problems with solutions pdf images are ready in this website. Graph coloring example problems with solutions pdf are a topic that is being searched for and liked by netizens now. You can Get the Graph coloring example problems with solutions pdf files here. Download all royalty-free photos and vectors.
If you’re looking for graph coloring example problems with solutions pdf pictures information linked to the graph coloring example problems with solutions pdf topic, you have visit the ideal blog. Our website always gives you suggestions for seeing the highest quality video and image content, please kindly surf and locate more informative video articles and graphics that match your interests.
Graph Coloring Example Problems With Solutions Pdf. Column Generation Integer Linear Programming Constraint Programming Graph Coloring. What is particularly striking is that Gerhard Ringel 1919 and J. To do this we can use Kuratowskis Theorem and nd either a K 33 or K 5 edge sub-division of the graphs. Graph Coloring and Scheduling Convert problem into a graph coloring problem.
Transformations Coloring Activity Color Activities Maths Activities Middle School Algebra Activities From pinterest.com
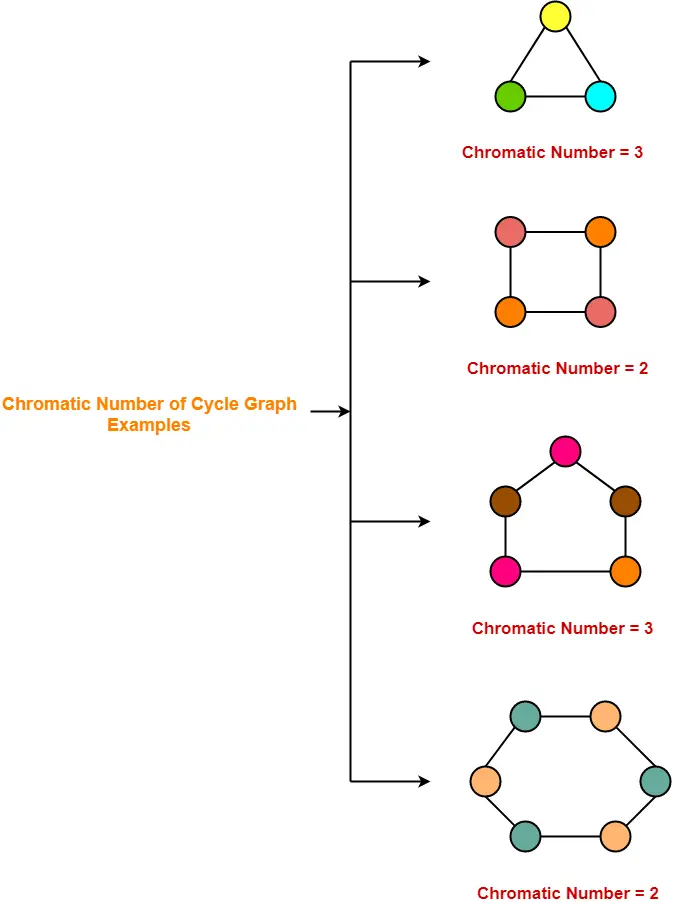
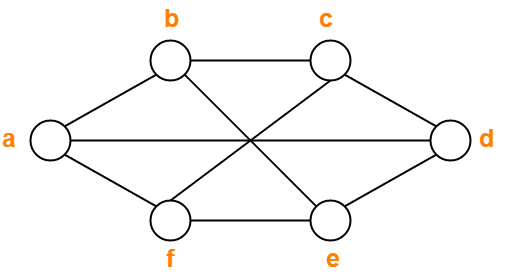
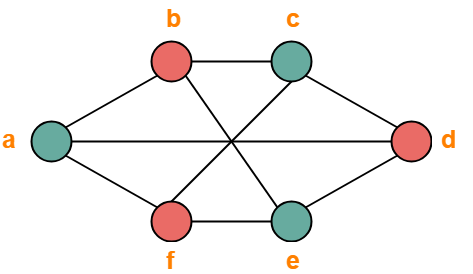
To do this we can use Kuratowskis Theorem and nd either a K 33 or K 5 edge sub-division of the graphs. Graph coloring problem is a NP Complete problem. Every bipartite graph which is having at least one edge has the chromatic number 2. We cannot use the same color for any adjacent vertices. Prove that a nite graph is bipartite if and only if it contains no cycles of odd length. Graph 1 Our example graph from earlier Graph 2 Solution.
Graph Coloring and Scheduling Convert problem into a graph coloring problem.
The first one is the most basic graph. Method to Color a Graph. Step 2 Choose the. The chromatic number is denoted by ꭓG. Constraint satisfaction problems n A CSP is composed of. But coloring has some constraints.
Source: gatevidyalay.com
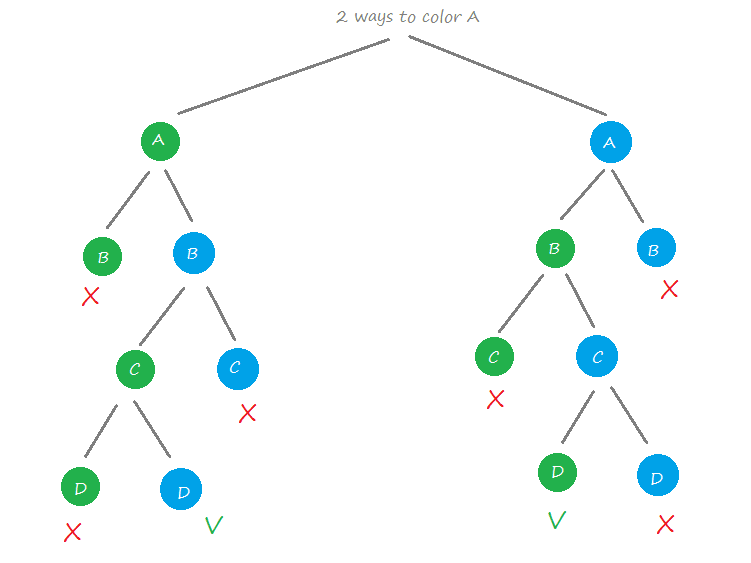
Step 1 Arrange the vertices of the graph in some order. Map coloring October 13 2014 3 Constraint satisfaction problems. The resulting graph is planar that is it can be drawn in the plane without any edges crossing. Here is a 4-coloring of the graph. GCP is very important because it has many applications.
Source: pinterest.com
The Graph k-Colorability Problem GCP can be stated as follows. Constraint Satisfaction Problems CSPs Russell and Norvig Chapter 6 CSP example. The Graph k-Colorability Problem GCP can be stated as follows. For solving this problem we need to use the greedy algorithm but it does not. Graph coloring problem is a special case of graph labeling.
Source: pinterest.com
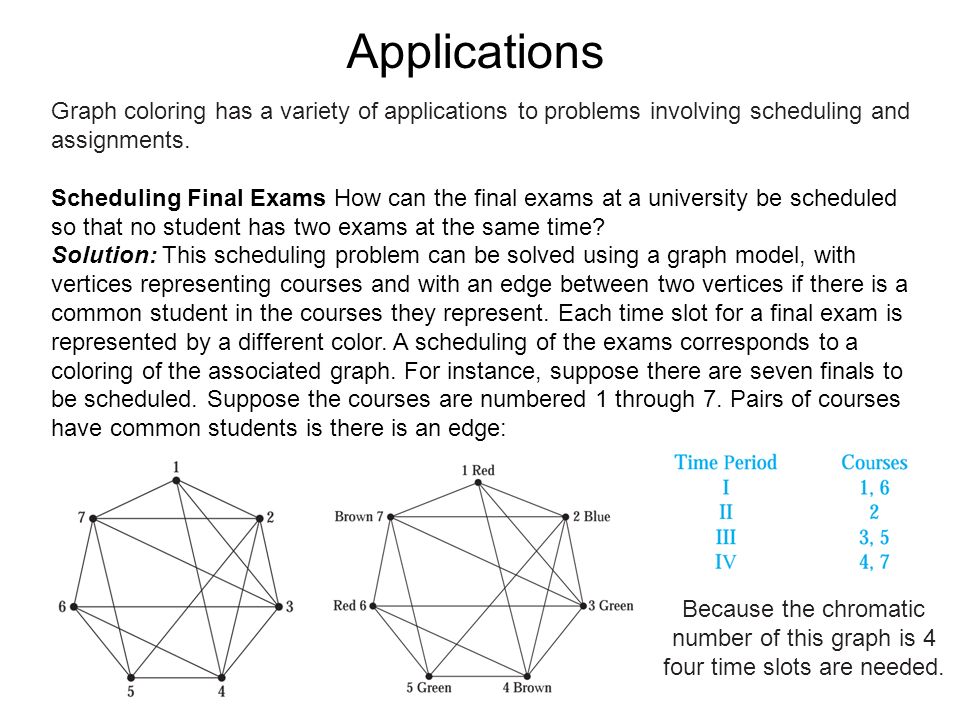
Q A set of variables X 1X 2X n with domains possible values D 1D 2D n q A set of constraints C 1C 2C m q Each constraint C i limits the values that a subset of variables can take eg V 1 V 2 In our example. Prove that if uis a vertex of odd degree in a graph then there exists a path from uto another. Here the colors would be schedule times such. 6Prove that the following graphs are non-planar. Example 582 If the vertices of a graph represent academic classes and two vertices are adjacent if the corresponding classes have people in common then a coloring of the vertices can be used to schedule class meetings.
Source: pdfprof.com
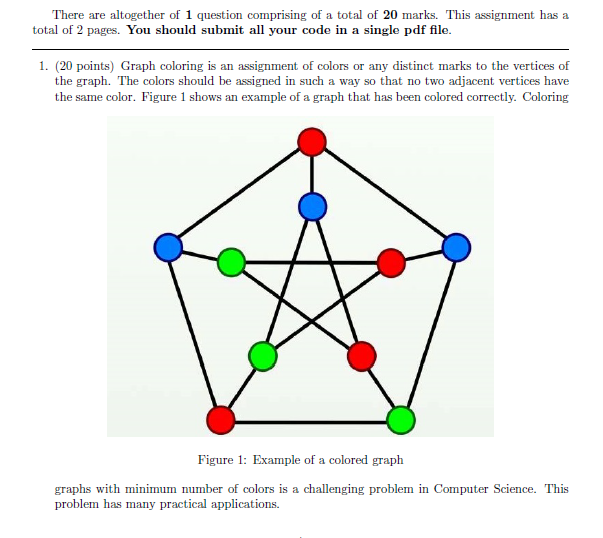
Example for propositional satisfiability SAT and graph coloring COL problems marginal prob- ability information about the uniform distribution over solutions or similar combinatorial objects has been the key ingredient in the success of BP-like algorithms. Constraint satisfaction problems n A CSP is composed of. G M I L A S H P C Question. Coloring A coloring of a simple graph is the assignment of a color to each vertex of the graph such that no two adjacent vertices are assigned the same color A simple solution to this problem is to color every vertex with a different color to get a total of colors. Every bipartite graph which is having at least one edge has the chromatic number 2.
Source: slideplayer.com
WA NT Q NSW V SA T n Domains. Prove that a nite graph is bipartite if and only if it contains no cycles of odd length. Graph coloring has many applications in addition to its intrinsic interest. So what we seek is a k-coloring of our graph with k as small as possible. They are of particular importance in modeling networks wherein they have applications in computer science biology sociology and many other areas.
Source: pinterest.com
Prove that a nite graph is bipartite if and only if it contains no cycles of odd length. Prove that a complete graph with nvertices contains nn 12 edges. The smallest number of colors required to color a graph G is called its chromatic number of that graph. Youngs 19101970 were able to prove in. They are of particular importance in modeling networks wherein they have applications in computer science biology sociology and many other areas.
Source: youtube.com
Youngs 19101970 were able to prove in. Constraint satisfaction problems n A CSP is composed of. Ships between pairs of objects. For the rst graph we nd a. The late nineteenth century saw more alleged solutions of the four-color problems many of which stood for as long as eleven years.
Source: pinterest.com
What is particularly striking is that Gerhard Ringel 1919 and J. Map coloring October 13 2014 3 Constraint satisfaction problems. They are of particular importance in modeling networks wherein they have applications in computer science biology sociology and many other areas. In this problem each node is colored into some colors. Is there a proper coloring that uses less than four colors.
Source: researchgate.net
Prove that if uis a vertex of odd degree in a graph then there exists a path from uto another. GCP is a NP-hard problem 1. A CSP is composed of. In this problem each node is colored into some colors. 1007 3137 3157 3203 4115 3261 4156 4118.
Source: interviewbit.com
A CSP is composed of. Two vertices are connected with an edge if the corresponding courses have a student in common. A k-coloring of a graph is a proper coloring involving a total of k colors. Colouring Bipartite Graphs A bipartite graph is a graph where we can split the vertices into two groups A and B and all of the edges have one endpoint in A and one in B. Graph coloring problem is a special case of graph labeling.
Source: researchgate.net
GCP is a NP-hard problem 1. Every bipartite graph which is having at least one edge has the chromatic number 2. Graph 1 Our example graph from earlier Graph 2 Solution. The steps required to color a graph G with n number of vertices are as follows. One example of a bipartite graph is K 33.
Source: gatevidyalay.com
The smallest number of colors required to color a graph G is called its chromatic number of that graph. For solving this problem we need to use the greedy algorithm but it does not. Graph coloring problem is a special case of graph labeling. The smallest number of colors required to color a graph G is called its chromatic number of that graph. Prove that if uis a vertex of odd degree in a graph then there exists a path from uto another.
Source: gatevidyalay.com
Two vertices are connected with an edge if the corresponding courses have a student in common. Some of them are planning and scheduling problems 23 timetabling 4 map coloring 5 and many others. Graph coloring problem is a special case of graph labeling. The solution approaches to a generalization of the problem known as Minimum Vertex Graph Multicoloring Problem where a given number of colors has to be assigned to each vertex. To do this we can use Kuratowskis Theorem and nd either a K 33 or K 5 edge sub-division of the graphs.
Source: pinterest.com
Given a graph G find xG and the corresponding coloring. This means that for any vertex in A all of the vertices it is adjacent to are in B. But in some cases the actual number of colors required could be less. Step 1 Arrange the vertices of the graph in some order. G M I L A S H P C Question.
Source: pinterest.com
The late nineteenth century saw more alleged solutions of the four-color problems many of which stood for as long as eleven years. Graphs are key objects studied in discrete mathematics. Graph 1 Our example graph from earlier Graph 2 Solution. The first one is the most basic graph. Is there a proper coloring that uses less than four colors.
Source: pencilprogrammer.com
This thesis focuses on four generalized graph coloring problems namely the graph color-ing problem GCP the equitable coloring problem ECP the weighted vertex coloring problem WVCP and the k-vertex critical subgraphs k-VCS. Prove that a nite graph is bipartite if and only if it contains no cycles of odd length. Q A set of variables X 1X 2X n with domains possible values D 1D 2D n q A set of constraints C 1C 2C m q Each constraint C i limits the values that a subset of variables can take eg V 1 V 2 In our example. For the rst graph we nd a. Given a graph G find xG and the corresponding coloring.
Source: wikiwand.com
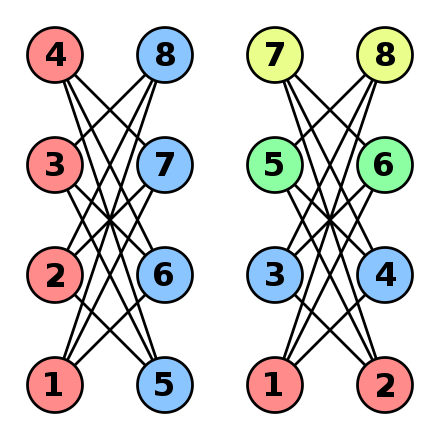
Different colors while optimizing a given optimization objective. The graphs that can be 1-colored are called edgeless graphs. G M I L A S H P C Question. Courses are represented by vertices. For the rst graph we nd a.
Source: br.pinterest.com
The resulting graph is planar that is it can be drawn in the plane without any edges crossing. G M I L A S H P C Question. Coloring A coloring of a simple graph is the assignment of a color to each vertex of the graph such that no two adjacent vertices are assigned the same color A simple solution to this problem is to color every vertex with a different color to get a total of colors. We focus on coloring problems which are problems concerning the partitions of a graph. Graph coloring has many applications in addition to its intrinsic interest.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring example problems with solutions pdf by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
