Your Graph coloring example problems with solutions images are available in this site. Graph coloring example problems with solutions are a topic that is being searched for and liked by netizens now. You can Find and Download the Graph coloring example problems with solutions files here. Get all royalty-free photos and vectors.
If you’re searching for graph coloring example problems with solutions pictures information connected with to the graph coloring example problems with solutions keyword, you have visit the right blog. Our site always gives you hints for viewing the maximum quality video and image content, please kindly hunt and locate more enlightening video articles and graphics that fit your interests.
Graph Coloring Example Problems With Solutions. This most basic variant of graph. For example consider the following two graphs. Step 1 Arrange the vertices of the graph in some order. This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other.
Graph Coloring Problem Techie Delight From techiedelight.com
For color in colors. Here the colors would be schedule times such. The steps required to color a graph G with n number of vertices are as follows. Step 2 Choose the first vertex and color it with the first color. Minimum number of colors used to color the given graph are 3. Step 1 Arrange the vertices of the graph in some order.
But if we consider the vertices 0 1 2 3 4 in right graph we need 4 colors.
This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other. Step 2 Choose the first vertex and color it with the first color. This thesis focuses on four generalized graph coloring problems namely the graph color-ing problem GCP the equitable coloring problem ECP the weighted vertex coloring problem WVCP and the k-vertex critical subgraphs k-VCS. Bool isBipartite vector. If we consider the vertices 0 1 2 3 4 in left graph we can color the graph using 3 colors. Figure15is an example of a Cartesian product of graphs.
Source: youtube.com
In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. Vertex coloring is the most commonly encountered graph coloring problem. Different colors while optimizing a given optimization objective. Note that in graph on right side vertices 3 and 4 are swapped. Constraint Programming is able.
Source: techiedelight.com
GCP is very important because it has many applications. The problem states that given m colors determine a way of coloring the vertices of a graph such that no two adjacent vertices are assigned same color. In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. Queue q. When solving the graph coloring problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints.
Source: researchgate.net
This most basic variant of graph. There is an edge between two vertices if they are in. Here the colors would be schedule times such. So the order in which the vertices are picked is important. For state in states.
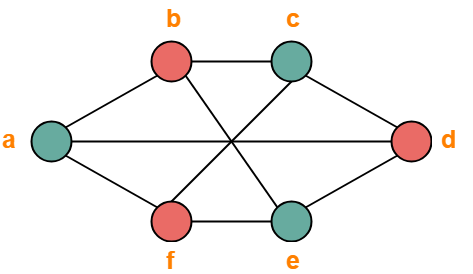Source: gatevidyalay.com
When solving the graph coloring problem with a mathematical optimization solver to avoid some symmetry in the solution space it is recommended to add the following constraints. I if colori -1 continue. For example consider the following two graphs. For int j 0. Bool isBipartite vector.
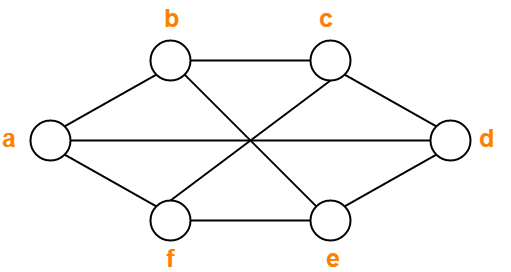Source: gatevidyalay.com
Queue q. We cannot use the same color for any adjacent vertices. Step 2 Choose the first vertex and color it with the first color. But if we consider the vertices 0 1 2 3 4 in right graph we need 4 colors. Colors_of_states def promising state color.
Source: codeproject.com
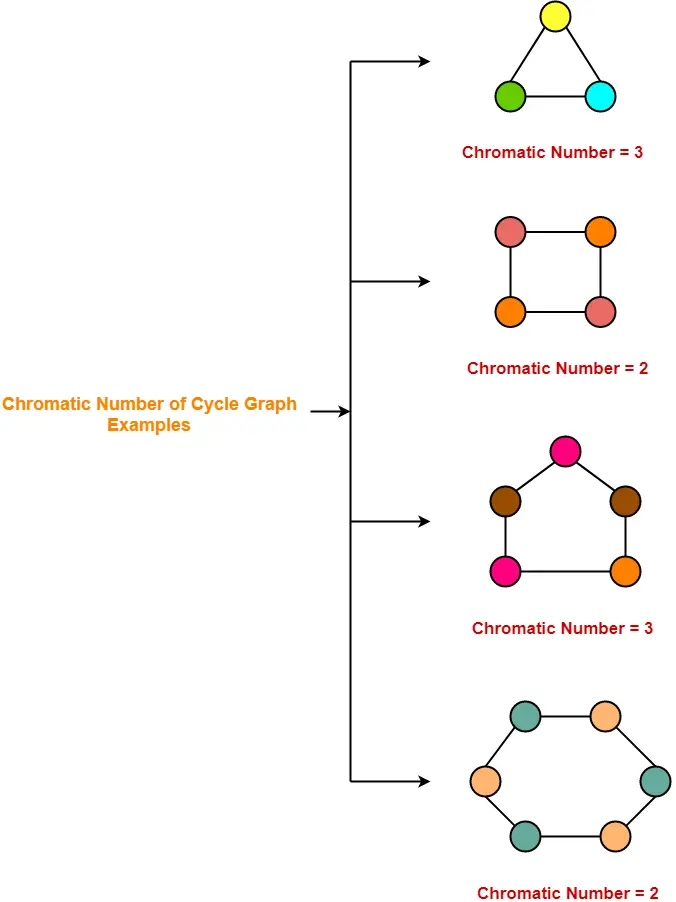
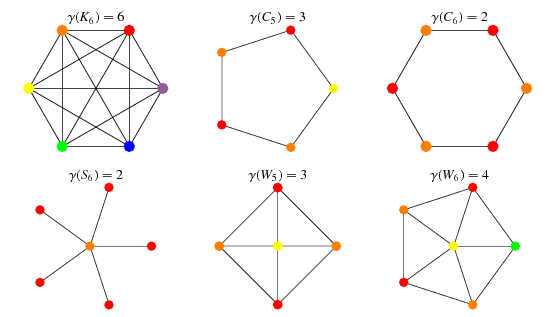
The smallest number of colors needed to color a graph G is called its chromatic number. Graph coloring problem is a special case of graph labeling. The smallest number of colors needed to color a graph G is called its chromatic number. This thesis focuses on four generalized graph coloring problems namely the graph color-ing problem GCP the equitable coloring problem ECP the weighted vertex coloring problem WVCP and the k-vertex critical subgraphs k-VCS. Bool isBipartite vector.
Source: techiedelight.com
In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. For int i 0. Applications of graph coloring. Graph coloring problem is a special case of graph labeling. The steps required to color a graph G with n number of vertices are as follows.
Source: slideshare.net
For graphs Gand H the Cartesian product G H is a graph whose vertex set is the. Step 2 Choose the first vertex and color it with the first color. This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other. Method to Color a Graph. Colors_of_states state get_color_for_state state.
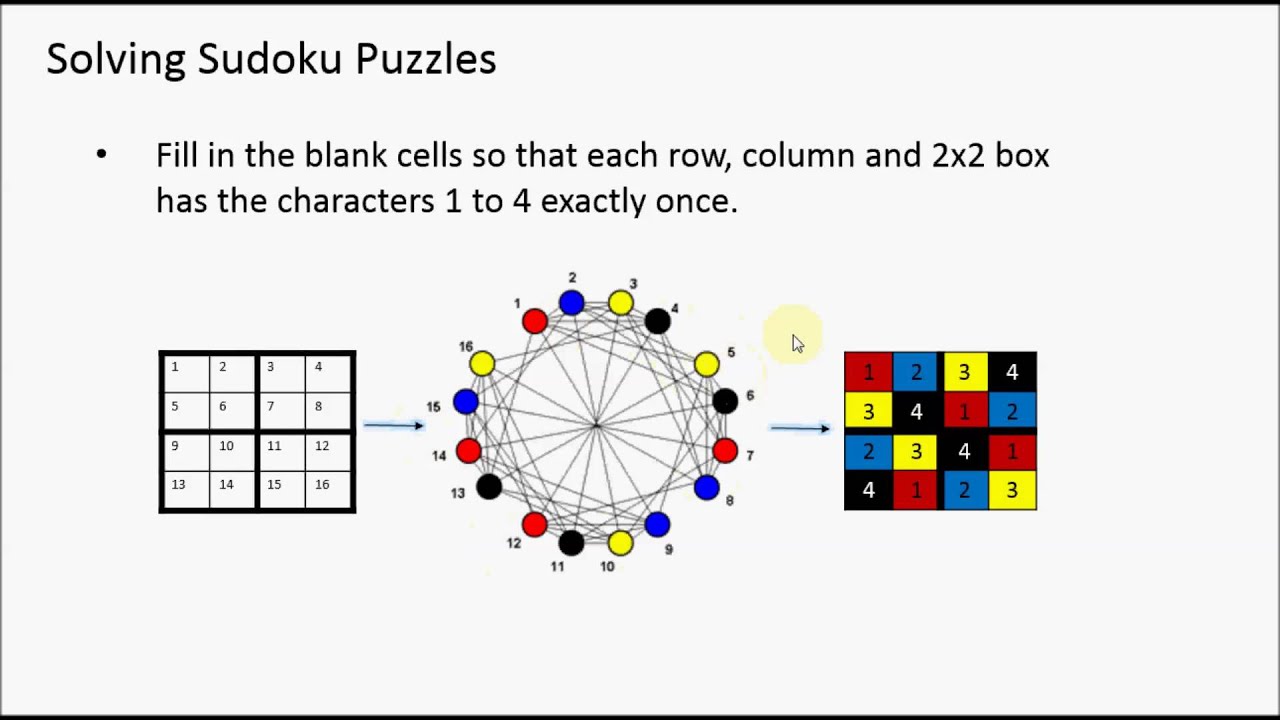Source: youtube.com
So the order in which the vertices are picked is important. In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. There is an edge between two vertices if they are in. Example 582 If the vertices of a graph represent academic classes and two vertices are adjacent if the corresponding classes have people in common then a coloring of the vertices can be used to schedule class meetings. Below is a sample graph coloring approach.
Source: researchgate.net
The smallest number of colors needed to color a graph G is called its chromatic number. Queue q. Here the colors would be schedule times such. What is the minimum number of frequencies needed. Continue try a different color for current vertex.
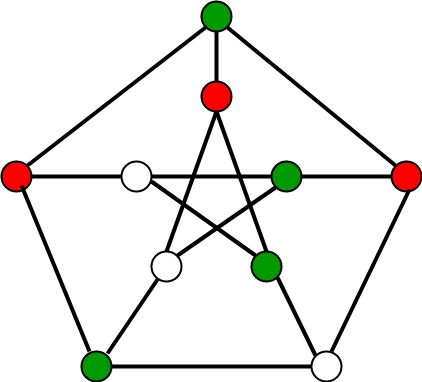Source: geeksforgeeks.org
Below is a sample graph coloring approach. There is an edge between two vertices if they are in. The smallest number of colors needed to color a graph G is called its chromatic number. Graph theory is an area of discrete mathematics with applications in a wide range of elds including computer science sociology and chemistry. The given graph may be properly colored using 3 colors as shown below- Problem-05.
Source: gatevidyalay.com
What is the minimum number of frequencies needed. GCP is very important because it has many applications. Figure15is an example of a Cartesian product of graphs. Note that in graph on right side vertices 3 and 4 are swapped. Example 582 If the vertices of a graph represent academic classes and two vertices are adjacent if the corresponding classes have people in common then a coloring of the vertices can be used to schedule class meetings.
Source: iq.opengenus.org
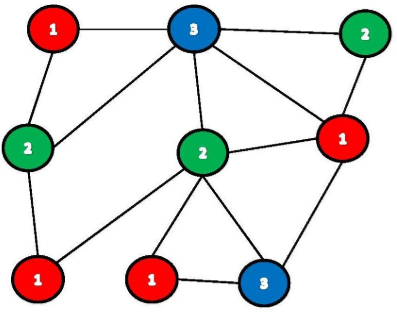
In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. Some of them are planning and scheduling problems 23 timetabling 4 map coloring 5 and many others. Vector colorn -1. For int i 0. The concept of graph coloring was introduced in order to solve the problem of coloring countries on a map so that no two countries that shared a border received the same color.
Source: youtube.com
Some of them are planning and scheduling problems 23 timetabling 4 map coloring 5 and many others. Step 2 Choose the first vertex and color it with the first color. The problem of coloring a graph arises in many practical areas such as pattern matching designing seating plans scheduling exam timetable solving Sudoku puzzles etc. For neighbor in neighbors. Different colors while optimizing a given optimization objective.
Source: mathworld.wolfram.com
Here the colors would be schedule times such. Vector colorn -1. The steps required to color a graph G with n number of vertices are as follows. The smallest number of colors required to color a graph G is called its chromatic number of that graph. Given a graph G find xG and the corresponding coloring.
Source: gatevidyalay.com
Therefore Chromatic Number of the given graph 3. Applications of graph coloring. Below is a sample graph coloring approach. The smallest number of colors required to color a graph G is called its chromatic number of that graph. Colors_of_states state get_color_for_state state.
Source: gatevidyalay.com
For state in states. Queue q. The problem of coloring a graph arises in many practical areas such as pattern matching designing seating plans scheduling exam timetable solving Sudoku puzzles etc. I if colori -1 continue. For int j 0.
Source: youtube.com
Figure15is an example of a Cartesian product of graphs. For int j 0. For int i 0. In this algorithm Step-12 Continue and Step-2 backtracking is causing the program to try different color option. If promising state color.
This site is an open community for users to share their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring example problems with solutions by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
