Your Graph coloring dynamic programming images are available in this site. Graph coloring dynamic programming are a topic that is being searched for and liked by netizens today. You can Find and Download the Graph coloring dynamic programming files here. Download all free images.
If you’re looking for graph coloring dynamic programming pictures information linked to the graph coloring dynamic programming topic, you have visit the ideal site. Our website frequently gives you suggestions for seeking the highest quality video and picture content, please kindly hunt and find more enlightening video articles and images that fit your interests.
Graph Coloring Dynamic Programming. TitleDynamic Algorithms for Graph Coloring. Color first vertex with first color. Dynamic graph coloring For each U V we find OPTU χGU the chromatic number of the subgraph induced by U Trivially OPTØ 0 For U 0 an optimal coloring consists of a maximal independent set I and an optimal coloring on the remaining vertices in GU I Thus OPTU is the minimum of 1 OPTU I over. Dynamic Algorithms for Graph Coloring.
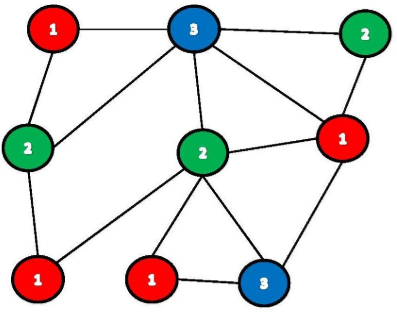
Graph Coloring Greedy Algorithm O V 2 E Time Complexity From iq.opengenus.org
Graph coloring Hamiltonian circuit etc. Dynamic Algorithms for Graph Coloring. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Given a tree color nodes black as many as possible without coloring two adjacent nodes Subproblems. Then Opt 0 OptS 1 minfOptS nI. Lawler4 was the first to propose a dynamic programming algorithm for the graph coloring problem as described in Algorithm 4.
In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color.
For the graph coloring problem. Dynamic Algorithms for Graph Coloring. For a good heuristic one may also choose a dynamic order. In graph theory graph coloring is a special case of graph labeling. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color. Color first vertex with first color.
Source: interviewbit.com
For the graph coloring problem. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color. Dynamic programming is a general-purpose AlgorithmDesignTechnique that is most often used to solve CombinatorialOptimization problems. Lawler4 was the first to propose a dynamic programming algorithm for the graph coloring problem as described in Algorithm 4. At any point color the uncolored vertex that currently has the highest number of different colors in its neighborhood.
Source: youtube.com
The smallest number of colors required to color a graph G is called its chromatic number of that graph. Approach of computing the answer to an instance of a problem. For any graph G there exists an optimal coloring for G where one color class is a maximal independent set in G. For every graph G there exists an order for V such that the greedy coloring algorithm uses exactly chiG colors. We present two algorithms that achieve different trade-offs between the number of recolorings and the number of colors used.
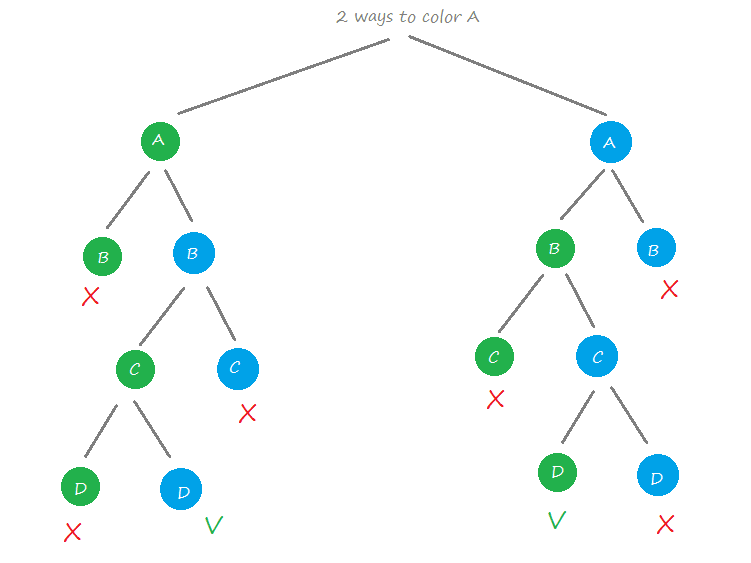Source: pencilprogrammer.com
TitleDynamic Algorithms for Graph Coloring. Dynamic programming is an algorithmic technique which is usually based on a recurrent formula and one or some starting states When its applied to graphs we can solve for the shortest. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. However most of these topics are outside the scope of this book and are actually worthy of having entire books dedicated specifically to their analysis. Graph Coloring is which type of algorithm design strategy – Backtacking – Greedy – Branch and Bound – Dynamic programming Design and Analysis of Algorithms Backtracking Algorithms.
Source: youtube.com
One may view his algorithm as based in the following result. Step 1 Arrange the vertices of the graph in some order. By computing and combining the answers to sub-instances. TitleDynamic Algorithms for Graph Coloring. Given a tree color nodes black as many as possible without coloring two adjacent nodes Subproblems.
Source: techiedelight.com
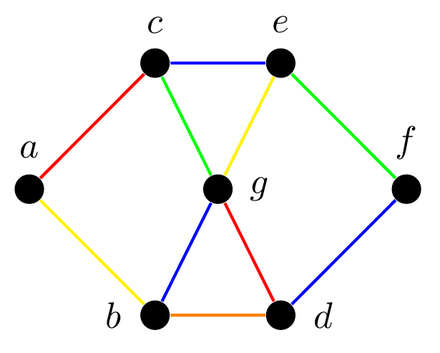
Similarly an edge coloring assigns a color to each edge so. Similarly an edge coloring assigns a color to each edge so. TitleDynamic Algorithms for Graph Coloring. In graph theory graph coloring is a special case of graph labeling. Here coloring of a graph means the assignment of colors to all vertices.
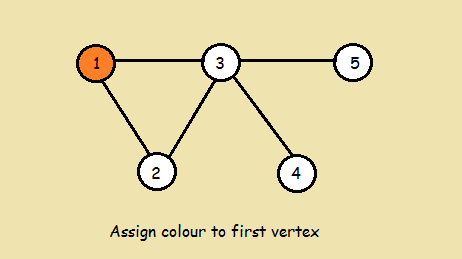Source: iq.opengenus.org
By computing and combining the answers to sub-instances. The optimal solution for a subtree having v as the root where we color v black W v. Dynamic programming is a general-purpose AlgorithmDesignTechnique that is most often used to solve CombinatorialOptimization problems. Exercise Dynamic Programming for Coloring GS subgraph of G induced by the vertices in S OptS minimum k such that GS is k-colorable. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors.
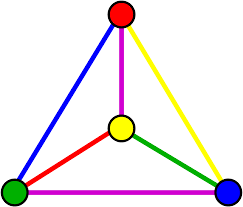Source: iq.opengenus.org
Graph coloring problem is a NP Complete problem. We present two algorithms that achieve different trade-offs between the number of recolorings and the number of colors used. Graph Coloring is which type of algorithm design strategy – Backtacking – Greedy – Branch and Bound – Dynamic programming Design and Analysis of Algorithms Backtracking Algorithms. First we arbitrarily decide the root node r B v. Dynamic Algorithms for Graph Coloring.
Source: iq.opengenus.org
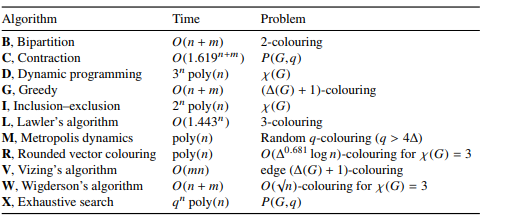
In the static setting there are simple linear time algorithms for - vertex coloring and -edge coloring in a graph with maximum degree. Similarly an edge coloring assigns a color to each edge so. For a good heuristic one may also choose a dynamic order. We present two algorithms that achieve different trade-offs between the number of recolorings and the number of colors used. For every graph G there exists an order for V such that the greedy coloring algorithm uses exactly chiG colors.
Source: geeksforgeeks.org
In the static setting there are simple linear time algorithms for - vertex coloring and -edge coloring in a graph with maximum degree. Recursively through the tree. For the graph coloring problem. For every graph G there exists an order for V such that the greedy coloring algorithm uses exactly chiG colors. Several problems commonly associated with graphs are identified as NP-complete graph coloring and the vertex cover problem to name two examples and can under the right circumstances be solved with dynamic programming.
Source: geeksforgeeks.org
SaturationColorsGivenagraphG andagraph coloringfforavertexu 2VGthesaturationcolorsofudenoted bySCuisthesetofcolorsthat f assignstousneighborsie SCu v2nbruvcolor. The smallest number of colors required to color a graph G is called its chromatic number of that graph. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. The optimal solution for a subtree having v as the root where we color v black W v. For any graph G there exists an optimal coloring for G where one color class is a maximal independent set in G.
Source: iq.opengenus.org
First we arbitrarily decide the root node r B v. Color first vertex with first color. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Tree DP Example Problem.
Source: gatevidyalay.com
At any point color the uncolored vertex that currently has the highest number of different colors in its neighborhood. Graph Coloring is which type of algorithm design strategy – Backtacking – Greedy – Branch and Bound – Dynamic programming Design and Analysis of Algorithms Backtracking Algorithms. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. This is called a vertex coloring. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
Source: link.springer.com
However most of these topics are outside the scope of this book and are actually worthy of having entire books dedicated specifically to their analysis. There are two parts to dynamic programming. Dynamic Algorithms for Graph Coloring. However most of these topics are outside the scope of this book and are actually worthy of having entire books dedicated specifically to their analysis. By computing and combining the answers to sub-instances.
Source: iq.opengenus.org
Exercise Dynamic Programming for Coloring GS subgraph of G induced by the vertices in S OptS minimum k such that GS is k-colorable. Basic Greedy Coloring Algorithm. Dynamic programming is a general-purpose AlgorithmDesignTechnique that is most often used to solve CombinatorialOptimization problems. Tree DP Example Problem. Color first vertex with first color.
Source: techiedelight.com
Dynamic Programming is the. Lawler4 was the first to propose a dynamic programming algorithm for the graph coloring problem as described in Algorithm 4. Dynamic graph coloring For each U V we find OPTU χGU the chromatic number of the subgraph induced by U Trivially OPTØ 0 For U 0 an optimal coloring consists of a maximal independent set I and an optimal coloring on the remaining vertices in GU I Thus OPTU is the minimum of 1 OPTU I over. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. Basic Greedy Coloring Algorithm.
Source: iq.opengenus.org
By computing and combining the answers to sub-instances. Tree DP Example Problem. One may view his algorithm as based in the following result. Graph coloring problem is a NP Complete problem. Graph coloring Hamiltonian circuit etc.
Source: youtube.com
Exercise Dynamic Programming for Coloring GS subgraph of G induced by the vertices in S OptS minimum k such that GS is k-colorable. Dynamic Algorithms for Graph Coloring. The optimal solution for a subtree having v as the root where we dont color v Answer is maxB. Graph coloring Hamiltonian circuit etc. For the graph coloring problem.
Source: geeksforgeeks.org
It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints. Graph coloring Hamiltonian circuit etc. The steps required to color a graph G with n number of vertices are as follows. Dynamic programming is an algorithmic technique which is usually based on a recurrent formula and one or some starting states When its applied to graphs we can solve for the shortest. Color first vertex with first color.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site helpful, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also save this blog page with the title graph coloring dynamic programming by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
