Your Graph coloring discrete mathematics images are ready in this website. Graph coloring discrete mathematics are a topic that is being searched for and liked by netizens today. You can Download the Graph coloring discrete mathematics files here. Get all free photos and vectors.
If you’re searching for graph coloring discrete mathematics pictures information related to the graph coloring discrete mathematics interest, you have pay a visit to the ideal blog. Our website always provides you with hints for seeing the highest quality video and image content, please kindly search and locate more enlightening video content and graphics that fit your interests.
Graph Coloring Discrete Mathematics. The Four color problem asks if it is possible to color every planar map by four colors. The chromatic number of a graph is the smallest number of colors with which it can be colored. In general given any graph Gtext a coloring of the vertices is called not surprisingly a vertex coloring. Planar Graphs Wikipedia Graph Coloring Wikipedia Discrete Mathematics and its Applications by Kenneth H Rosen.
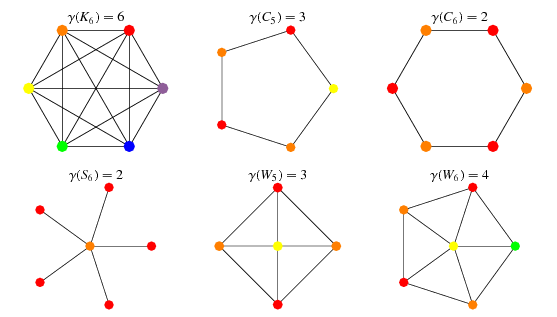Chromatic Number From Wolfram Mathworld From mathworld.wolfram.com
This is because for every k -colouring of G 1 x and y must get different colours say x red and y blue. Of Edinburgh UK Discrete Mathematics Chapter 6 2 13. The vertices of the graph represent the players and the edges represent the matches that need to be played. In an optimal coloring. The m-Coloring optimization problem Objective. Properly coloring of a graph Painting all the vertices of a graph with colours such that no two adjacent vertices have the same colour is called the proper colouring or simply colouring of a graph.
As the second graph T_m is 2-colorable once we colored one single vertex with a color we can complete it to a 2-coloring of this T_m.
The vertex you picked from this graph has one color. In this note we state how correspondence colorings. Give each vertex one color for initialization. For example you could color every vertex with a different color. Some areas include graph theory networks counting techniques coloring theory game theory and more. In general given any graph Gtext a coloring of the vertices is called not surprisingly a vertex coloring.
Source: youtube.com
The vertex you picked from this graph has one color. The chromatic number of a graph is the smallest number of colors with which it can be colored. The objective is to minimize. For coloring visit each vertex and check each. The Four color problem asks if it is possible to color every planar map by four colors.
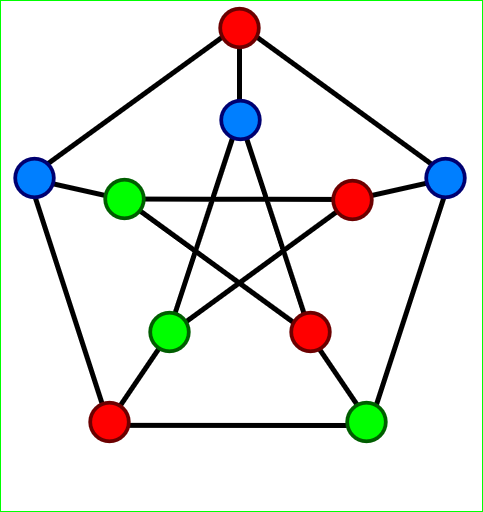Source: medium.com
A graph in which every vertex has been assigned a colour according to a proper colouring is called a properly coloured graph. Properly coloring of a graph Painting all the vertices of a graph with colours such that no two adjacent vertices have the same colour is called the proper colouring or simply colouring of a graph. Graph Coloring Algorithm. Find all the symmetric edges in one representation of i j and j i. Kim and Ozeki observed that correspondence colorings generalize various notions of signed-graph colorings which again generalizes ordinary graph colorings.
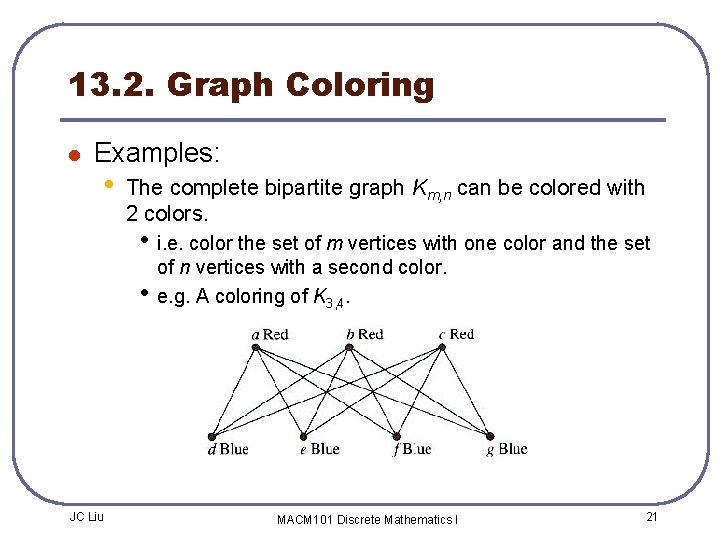Source: slidetodoc.com
Every graph has a proper vertex coloring. Minimize the number of colors used. As the second graph T_m is 2-colorable once we colored one single vertex with a color we can complete it to a 2-coloring of this T_m. The chromatic number of a graph is the smallest number of colors with which it can be colored. T G k 1 k k 1 T G 1 k T G 2 k.
Source: youtube.com
Informally a graph consists of a non-empty set of vertices or nodes. A graph has been colored if a color has been assigned to each vertex in such a way that adjacent vertices have different colors. If the vertex coloring has the property that adjacent vertices are colored differently then the coloring is called proper. Color the vertex picked from the second graph with the other color. Kim and Ozeki observed that correspondence colorings generalize various notions of signed-graph colorings which again generalizes ordinary graph colorings.
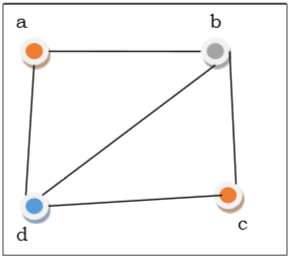Source: tutorialspoint.com
Color the vertex picked from the second graph with the other color. In an optimal coloring there must be at least one of the graphs m edges between every pair of color classes. Suppose you have been given the job of scheduling a round-robin tennis tournament with n players. Ill break it down and make every part more clear. T G k 1 k k 1 T G 1 k T G 2 k.
Source: youtube.com
The Four color problem asks if it is possible to color every planar map by four colors. Minimize the number of colors used. Color the vertex picked from the second graph with the other color. Brief look at other topics like graph coloring Kousha Etessami U. In an optimal coloring there must be at least one of the graphs m edges between every pair of color classes.
Source: mathworld.wolfram.com
Coloring A coloring of a simple graph is the assignment of a color to each vertex of the graph such that no two adjacent vertices are assigned the same color A simple solution to this problem is to color every vertex with a different color to get a total of colors. It has roots in the Four color problem which was the central problem of graph coloring in the last century. A graph in which every vertex has been assigned a colour according to a proper colouring is called a properly coloured graph. Please write comments if you find anything incorrect or you want to share more information about the topic discussed above. Graph coloring is a popular topic of discrete mathematics.
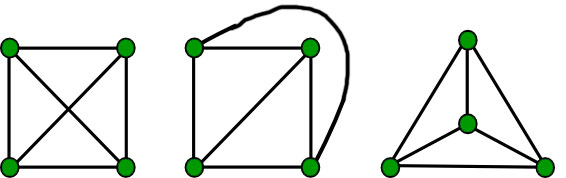Source: geeksforgeeks.org
Map Coloring to Graph Coloring Part of a unit on discrete mathematics. In this note we state how correspondence colorings. A graph in which every vertex has been assigned a colour according to a proper colouring is called a properly coloured graph. Yes if you have a graph G made of two graphs G 1 and G 2 which have precisely two vertices x y and an edge x y in common then. Every graph has a proper vertex coloring.
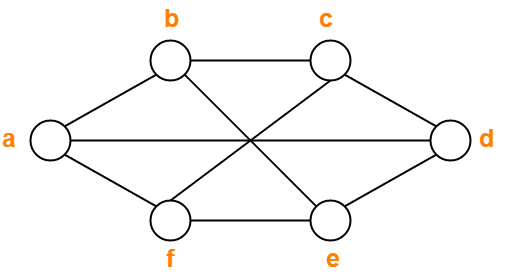Source: gatevidyalay.com
One way to approach the problem is to model it as a graph. This is because for every k -colouring of G 1 x and y must get different colours say x red and y blue. Color the vertex picked from the second graph with the other color. Graph is an assignment of colors either to the vertices of the graphs or. In an optimal coloring.
Source: slideplayer.com
Yes if you have a graph G made of two graphs G 1 and G 2 which have precisely two vertices x y and an edge x y in common then. In general given any graph Gtext a coloring of the vertices is called not surprisingly a vertex coloring. It is the mathematics of computers. As the second graph T_m is 2-colorable once we colored one single vertex with a color we can complete it to a 2-coloring of this T_m. Brief look at other topics like graph coloring Kousha Etessami U.
Source: study.com
Although it is claimed to the Four color. Coloring A coloring of a simple graph is the assignment of a color to each vertex of the graph such that no two adjacent vertices are assigned the same color A simple solution to this problem is to color every vertex with a different color to get a total of colors. But in some cases the actual number of colors required could be less than this. Graph is an assignment of colors either to the vertices of the graphs or. Give each vertex one color for initialization.
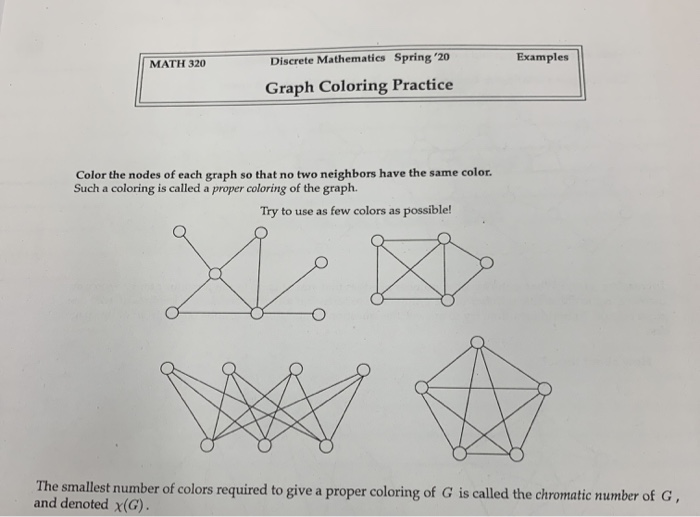Source: chegg.com
To complete the proof it is easy to argue that the graph is not one -colorable. Suppose you have been given the job of scheduling a round-robin tennis tournament with n players. Proper coloring of a. T G k 1 k k 1 T G 1 k T G 2 k. What is a Graph.
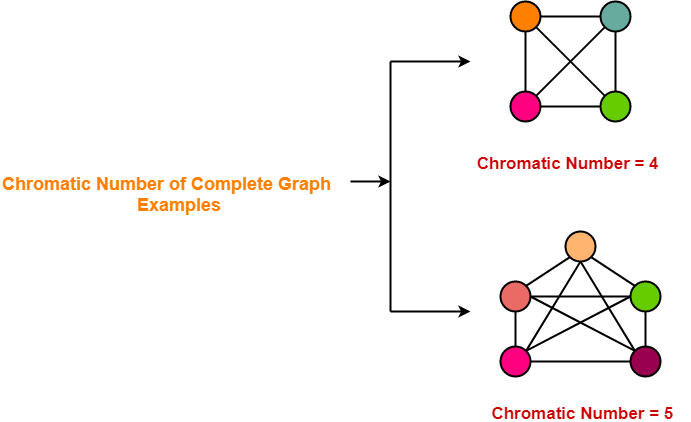Source: gatevidyalay.com
The vertices of the graph represent the players and the edges represent the matches that need to be played. Yes if you have a graph G made of two graphs G 1 and G 2 which have precisely two vertices x y and an edge x y in common then. Ill break it down and make every part more clear. The chromatic number of a graph is the smallest number of colors with which it can be colored. If the vertex coloring has the property that adjacent vertices are colored differently then the coloring is called proper.
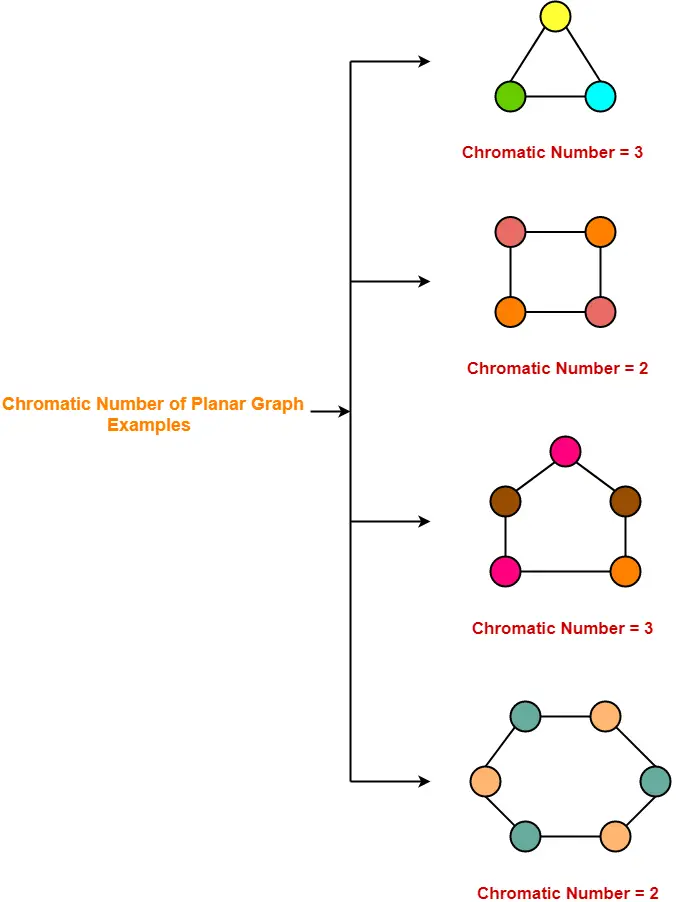Source: gatevidyalay.com
In general given any graph Gtext a coloring of the vertices is called not surprisingly a vertex coloring. The objective is to minimize. Some areas include graph theory networks counting techniques coloring theory game theory and more. Informally a graph consists of a non-empty set of vertices or nodes. Proper coloring of a.
Source: slideplayer.com
Of Edinburgh UK Discrete Mathematics Chapter 6 2 13. Yes if you have a graph G made of two graphs G 1 and G 2 which have precisely two vertices x y and an edge x y in common then. Properly coloring of a graph Painting all the vertices of a graph with colours such that no two adjacent vertices have the same colour is called the proper colouring or simply colouring of a graph. For example you could color every vertex with a different color. Graph coloring is a popular topic of discrete mathematics.
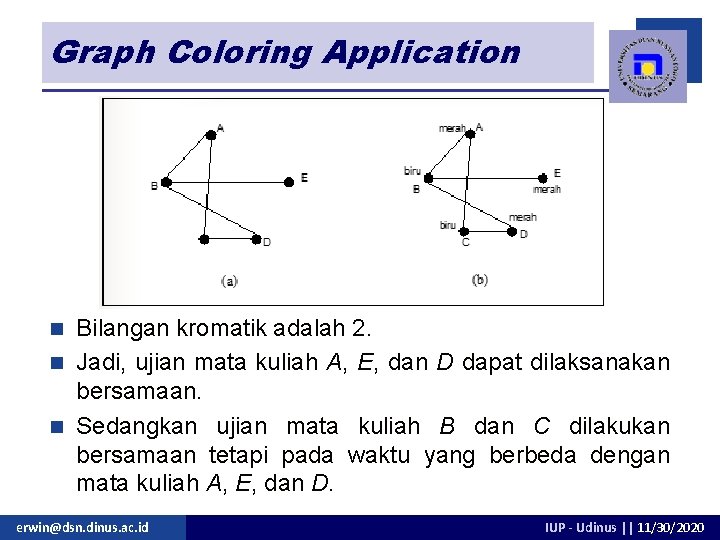Source: slidetodoc.com
It has roots in the Four color problem which was the central problem of graph coloring in the last century. Color the vertex picked from the second graph with the other color. To the edges in suc h a w a y that adjacent vertices edges are colored. To complete the proof it is easy to argue that the graph is not one -colorable. Suppose you have been given the job of scheduling a round-robin tennis tournament with n players.
Source: slidetodoc.com
Proper coloring of a. A graph in which every vertex has been assigned a colour according to a proper colouring is called a properly coloured graph. Every graph has a proper vertex coloring. If the vertex coloring has the property that adjacent vertices are colored differently then the coloring is called proper. Every graph has a proper vertex coloring.
Source: geeksforgeeks.org
Every graph has a proper vertex coloring. A graph in which every vertex has been assigned a colour according to a proper colouring is called a properly coloured graph. Ill break it down and make every part more clear. One way to approach the problem is to model it as a graph. Since it is a round-robin tournament every player must play.
This site is an open community for users to submit their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site beneficial, please support us by sharing this posts to your preference social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring discrete mathematics by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
