Your Graph coloring decision problem images are ready in this website. Graph coloring decision problem are a topic that is being searched for and liked by netizens today. You can Download the Graph coloring decision problem files here. Get all free photos.
If you’re looking for graph coloring decision problem images information related to the graph coloring decision problem interest, you have come to the right blog. Our website frequently gives you suggestions for seeing the maximum quality video and picture content, please kindly surf and find more enlightening video content and graphics that fit your interests.
Graph Coloring Decision Problem. As mentioned the general problem is np-complete. This graph coloring problem is also known as M-colorability decision problem. Two adjacent vertices are in conflict if they have the same color. Our proposed model leverages the specific features of such problem by adding internal representations of vertices and colors to the GNN kernel and by performing messagepassing iterations over such representations.
Five Phases Of Organizational Growth Study Creative Problem Solving Design Theory From pinterest.com
It is also true that planar graphs graphs that do not contain K33 or K5 as sub graphs as per Kuratowskis theorem can be colored with 4 colors. This length is given by one or two parameters for example in the graph coloring problem the number of vertices of the graph. In this problem each node is colored into some colors. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict. As mentioned the general problem is np-complete.
For example if the vertices of a graph represent traffic signals at an intersection and two vertices are adjacent if the corresponding signals.
Show that your deci-sion problem is solvable in polynomial time if and only if the graph-coloring problem is solvable in polynomial time. The M-colorability Decision Problem comes under the concept of graph coloring. Given a graph G find xG and the corresponding coloring. We cannot use the same color for any adjacent vertices. The difficulty of a problem is related to its structure and the length of the instance to be considered. In this problem each node is colored into some colors.
Source: pinterest.com
Let the language 3-COLOR be the set of graphs that can be3-colored. Our proposed model leverages the specific features of such problem by adding internal representations of vertices and colors to the GNN kernel and by performing messagepassing iterations over such representations. The M-colorability Decision Problem comes under the concept of graph coloring. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be. Difficulty Level.
Source: pinterest.com
A statement of what properties the answer or solution is required to satisfy. Let the language 3-COLOR be the set of graphs that can be3-colored. The difficulty of a problem is related to its structure and the length of the instance to be considered. Here coloring of a graph means the assignment of colors to all vertices. The other graph coloring problems like Edge Coloring No vertex is incident to two edges of same color and Face Coloring Geographical Map Coloring can be transformed into vertex coloring.
Source: pinterest.com
Show that if 3-COLOR is NP-complete then your decision problem from part b is. Show that your decision problem is solvable in polynomial time if and only of the graph-coloring problem is solvable in polynomial time b. The other graph coloring problems like Edge Coloring No vertex is incident to two edges of same color and Face Coloring Geographical Map Coloring can be transformed into vertex coloring. Given a graph G find xG and the corresponding coloring. As mentioned the general problem is np-complete.
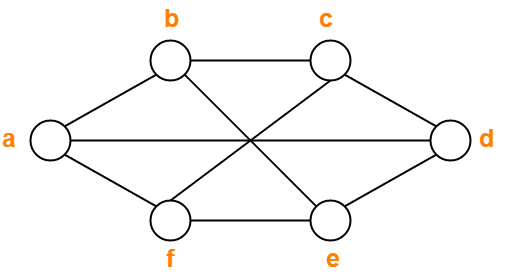Source: gatevidyalay.com
The Graph k-Colorability Problem GCP can be stated as follows. T has been proven that 3-COLOR is. Some of them are planning and scheduling problems 23 timetabling 4 map coloring 5 and many others. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. A proper coloring of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color.
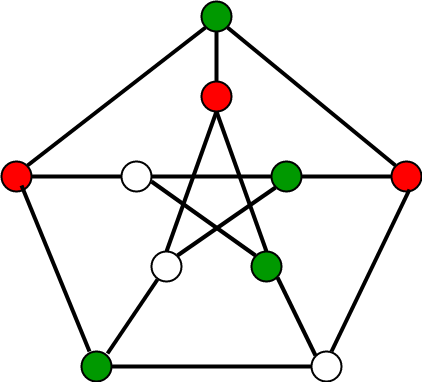Source: geeksforgeeks.org
Here coloring of a graph means the assignment of colors to all vertices. Bipartite graphs can be colored using only 2 colors. Our proposed model leverages the specific features of such problem by adding internal representations of vertices and colors to the GNN kernel and by performing messagepassing iterations over such representations. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be.
Source: pinterest.com
GCP is a NP-hard problem 1. Proving NP-completeness of a graph coloring problem. But coloring has some constraints. Some of them are planning and scheduling problems 23 timetabling 4 map coloring 5 and many others. Then we make at most n calls to the oracle.
Source: pinterest.com
T has been proven that 3-COLOR is. Difficulty Level. The Graph Coloring decision problem is np-complete ie asking for existence of a coloring with less than q colors as given a coloring it can be easily checked in polynomial time whether or not it uses less than q colors. As mentioned the general problem is np-complete. Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color.
Source: pinterest.com
Show that if 3-COLOR is NP-complete then your decision problem from part b is. Show that your decision problem is solvable in polynomial time if and only of the graph-coloring problem is solvable in polynomial time b. For the first part we can perform a search to find the optimal k. Find a assignment of colors to vertices that minimizes the number of adjacent vertices in conflict. In this dissertation we are specifically concerned with the application of a GNN model to tackle the graph coloring problem.
Source: geeksforgeeks.org
It is also true that planar graphs graphs that do not contain K33 or K5 as sub graphs as per Kuratowskis theorem can be colored with 4 colors. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be. For solving this problem we need to use the greedy algorithm but it does not guaranty to use minimum color. Find chromatic number of the following graph- Solution- Applying Greedy Algorithm Minimum number of colors required to color the given graph are 3. Graph coloring problem is a special case of graph labeling.
Source: pinterest.com
Let the language 3-COLOR be the set of graphs that can be 3-colored. For the first part we can perform a search to find the optimal k. The other graph coloring problems like Edge Coloring No vertex is incident to two edges of same color and Face Coloring Geographical Map Coloring can be transformed into vertex coloring. Two adjacent vertices are in conflict if they have the same color. On the other hand the Graph Coloring Optimisation problem which aims to find the coloring with minimum colors is np-hard because even if you are given a coloring you will not be.
Source: geeksforgeeks.org
The graph-coloring problem is to determine the minimum number of colors needed to color a given graph. For the first part we can perform a search to find the optimal k. Here coloring of a graph means the assignment of colors to all vertices. Graph Neural Network architecture to solve the decision version of the graph coloring problem GCP machine-reasoning-ufrgsgithubiognn-gcp 9 stars 5 forks. GCP is a NP-hard problem 1.
Source: id.pinterest.com
Show that if 3-COLOR is NP-complete then your decision problem from part b is. State the graph-coloring problem as a decision problem K-COLOR. Here coloring of a graph means the assignment of colors to all vertices. For solving this problem we need to use the greedy algorithm but it does not guaranty to use minimum color. Bipartite graphs can be colored using only 2 colors.
Source: id.pinterest.com
T has been proven that 3-COLOR is. Here coloring of a graph means the assignment of colors to all vertices. As mentioned the general problem is np-complete. A statement of what properties the answer or solution is required to satisfy. In this dissertation we are specifically concerned with the application of a GNN model to tackle the graph coloring problem.
Source: pinterest.com
Difficulty Level. But coloring has some constraints. It is also true that planar graphs graphs that do not contain K33 or K5 as sub graphs as per Kuratowskis theorem can be colored with 4 colors. We cannot use the same color for any adjacent vertices. As mentioned the general problem is np-complete.
Source: pinterest.com
GCP is a NP-hard problem 1. A proper coloring of a graph is an assignment of colors to the vertices of the graph so that no two adjacent vertices have the same color. Show that if 3-COLOR is NP-complete then your decision problem from part b is. In this dissertation we are specifically concerned with the application of a GNN model to tackle the graph coloring problem. Show that your decision problem is solvable in polynomial time if and only of the graph-coloring problem is solvable in polynomial time b.
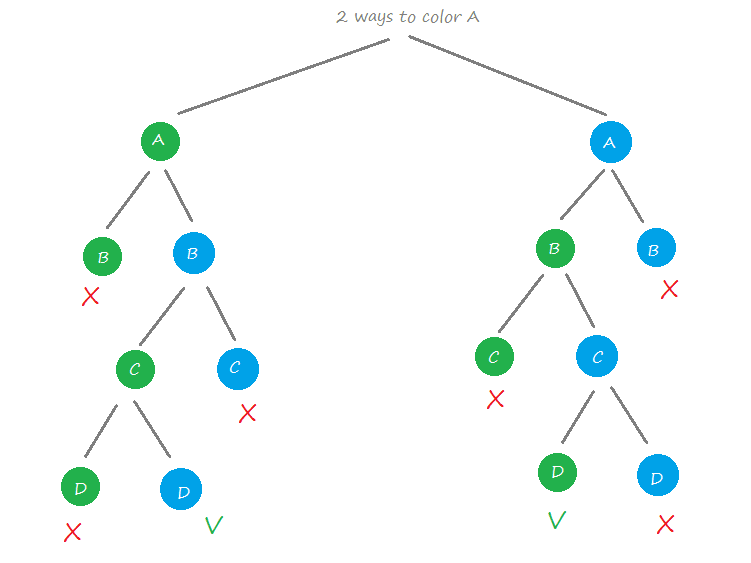Source: pencilprogrammer.com
Cast the graph-coloring problem as a decision problem. For the first part we can perform a search to find the optimal k. A statement of what properties the answer or solution is required to satisfy. Show that if 3-COLOR is NP-complete then your decision problem from part b is. If we have an oracle for the decision version of the colouring problem we can do both.
Source: pinterest.com
In this problem each node is colored into some colors. Given a graph G find xG and the corresponding coloring. Cast the graph-coloring problem as a decision problem. But coloring has some constraints. Show that your decision problem is solvable in polynomial time if and only of the graph-coloring problem is solvable in polynomial time b.
Source: in.pinterest.com
Given an undirected graph and a number m determine if the graph can be coloured with at most m colours such that no two adjacent vertices of the graph are colored with the same color. This length is given by one or two parameters for example in the graph coloring problem the number of vertices of the graph. We cannot use the same color for any adjacent vertices. Proving NP-completeness of a graph coloring problem. Difficulty Level.
This site is an open community for users to do submittion their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site good, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title graph coloring decision problem by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
